Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Trải 4 mặt của hình chóp ra mặt phẳng và tìm điều kiện để A M + M N + N P + P Q là nhỏ nhất.
Cách giải:
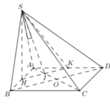
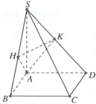
Ta “xếp” 4 mặt của hình chóp lên một mặt phẳng, được như hình bên:
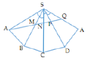
Như hình vẽ ta tháy, để tiết kiệm dây nhất thì các đoạn AM, MN, NP, PQ phải tạo thành một đoạn thẳng AQ.
Lúc này, xét Δ S A Q có:
A S M = M S N = N S P = P S Q = 15 °
S A = 600 m , S Q = 300 m
⇒ k = A M + M N N P + P Q = A N N Q = S A S Q = 2
(Vì A N N Q = S A S Q do tính chất của đường phân giác SN).

Đáp án B
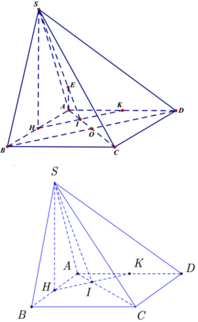
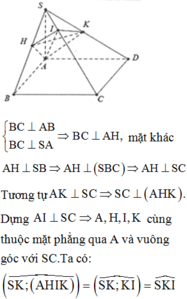
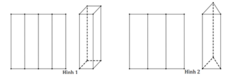
Trải hình ra ta thu được:
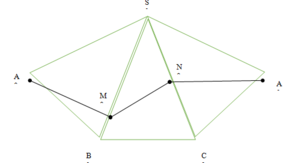
Dễ thấy AM + MN + NA đạt giá trị nhỏ nhất khi A, M, N, A thẳng hàng
Lại có S.ABC là hình chóp tam giác đều
ð ∆SAB = ∆SBC = ∆SAC (c.c.c)
⇒ AS B ^ = B S C ^ = C S A ^ ⇒ AS A ^ = 90 °
AM + MN + N A m i n = a 2
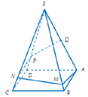
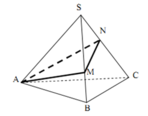






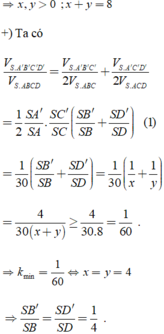


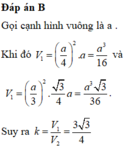
Đáp án B
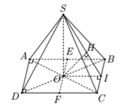
Gọi F’,H’ là điểm đối xứng của F,H qua SO
( O là tâm của đáy)
⇒ EF'=EF, FH=F'H'
Gọi I,J là điểm đối xứng của A,F’ qua SB
⇒ EF ' = EJ , F ' H ' = H ' J
A E + EF'+F'H'+H'K=AE+EJ + H ' J + H ' K ≥ AJ + K J
Gọi R là điểm đối xứng của A qua SI ⇒ AJ = J R
⇒ AJ + K J = J R + K J ≥ K R
Vậy để AE+EF’+F’H’+H’K nhỏ nhất bằng KR thì
H ' J + H ' K = K J A E + EJ = AJ = J R
k = H F + H K E A + EF = H ' F ' + H ' K E A + EF' = K J J R = S K S A = 1 2