Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhiệt lượng quả cầu nhôm tỏa ra:
\(Q_{tỏa}=m_{Al}\cdot c_{Al}\cdot\left(t_1-t\right)\)
\(=0,15\cdot880\cdot\left(100-25\right)=9900J\)
Nhiệt lượng nước đã thu vào:
\(Q_{thu}=m_{nc}\cdot c_{nc}\cdot\left(t-t_2\right)\)
\(=m_{nc}\cdot4200\cdot\left(25-20\right)=21000m_{nc}\left(J\right)\)
Cân bằng nhiệt: \(Q_{thu}=Q_{tỏa}\)
\(\Rightarrow21000m_{nc}=9900\)
\(\Rightarrow m_{nc}=0,47kg\)
Không có đáp án

Ta có:
Nhôm m 1 = 0 , 15 c 1 = 880 J / k g . K t 1 = 100 o C
Nước m 2 = ? c 2 = 4200 J / k g . K t 2 = 20 o C
Nhiệt độ cân bằng t = 25°C
Nhiệt lượng mà quả cầu nhôm tỏa ra là: Q1 = m1c1(t1 – t)
Nhiệt lượng mà nước nhận được là: Q2 = m2c2(t – t2)
Áp dụng phương trình cân bằng nhiệt, ta có:
Q1 = Q2 ⇔ m1c1(t1 – t) = m2c2(t – t2)
⇔ 0,15.880.(100 – 25) = m2.4200.(25 – 20)
⇔ m2 = 0,471 kg
⇒ Đáp án B

a.
Cân bằng nhiệt:
\(Q_{thu}=Q_{toa}=mc\left(t_1-t\right)=0,15\cdot880\cdot\left(100-25\right)=9900\left(J\right)\)
b.
Ta có: \(Q_{thu}=mc\left(t-t_1\right)\)
\(\Leftrightarrow9900=m\cdot4200\cdot\left(25-20\right)\)
\(\Leftrightarrow m\approx0,5\left(kg\right)\)
Ta có: \(m=DV\Rightarrow V=\dfrac{m}{D}=\dfrac{0,5}{1000}=5\cdot10^{-4}\left(m^3\right)\)

a) Ta có: \(Q_{tỏa}=m_{Al}\cdot c_{Al}\cdot\Delta t=0,2\cdot880\cdot\left(100-27\right)=12848\left(J\right)\)
b) Ta có: \(Q_{thu}=Q_{tỏa}=12848\left(J\right)\)
\(\Rightarrow m_{nước}\cdot c_{nước}\cdot\Delta t'=m_{nước}\cdot4200\cdot\left(27-20\right)=12848\left(J\right)\)
\(\Rightarrow m_{nước}\approx0,437\left(kg\right)=4,37\cdot10^{-4}\left(m^3\right)\)

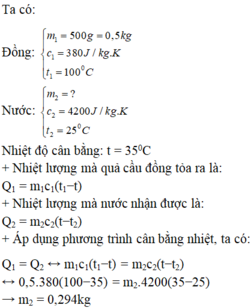
a.
Cân bằng nhiệt: \(Q_{thu}=Q_{toa}\)
\(\Leftrightarrow1\cdot4200\cdot\left(t-20\right)=0,5\cdot880\cdot\left(100-t\right)\)
\(\Leftrightarrow4200t-84000=44000-440t\)
\(\Leftrightarrow t\approx27,6^0C\)
Vậy sau 1 thời gian, nhiệt độ của quả cầu là 72,4 độ C và nước là 27,6 độ C
b.
Ta có: \(80\%Q_{toa}=Q_{thu}\)
\(\Leftrightarrow80\%\cdot0,5\cdot880\cdot\left(100-t\right)=1\cdot4200\cdot\left(t-20\right)\)
\(\Leftrightarrow35200-352t=4200t-84000\)
\(\Leftrightarrow t=26,2^0C\)
Nhiệt độ nước khi đó là 26,2 độ C
Cảm ơn bạn