Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`[2-x]/x >= 1`
`<=>[2-x-x]/x >= 0`
`<=>[2-2x]/x >= 0`
`<=>0 < x <= 1`
`->\bb B`

\(5x-1>2x+3\)
\(\Leftrightarrow5x-2x>3+1\)
\(\Leftrightarrow3x>4\)
\(\Leftrightarrow x>\dfrac{4}{3}\)
--> Chọn C

Đặt \(f\left(x\right)=\dfrac{x-1}{\left(x-2\right)\left(x-3\right)}.\)
\(x-1=0.\Leftrightarrow x=1.\\ x-2=0.\Leftrightarrow x=2.\\ x-3=0.\Leftrightarrow x=3.\)
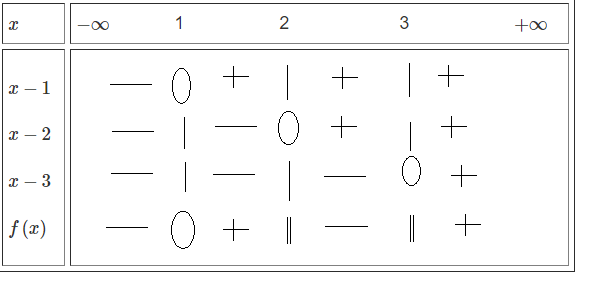
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\) \(\left(1;2\right)\cup\left(3;+\infty\right).\)
\(\Rightarrow B.\)

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)

`[2-x]/[x+3] > x+1` `ĐK: x \ne -3`
`=>` Loại đ/á `\bb A`
Thay `x=-1` vào bất ptr có: `1,5 > 0` (Luôn đúng) `->\bb B` t/m
Thay `x=2` vào bất ptr có: `0 > 3` (Vô lí) `->\bb C` loại
Thay `x=0` vào bất ptr có: `2/3 > 1` (Vô lí) `->\bb D` loại
______________________________________________________
`=>` Chọn `\bb B`

Câu 8:
$(x-1)(2+x)>0$ thì có 2 TH xảy ra:
TH1: \(\left\{\begin{matrix} x-1>0\\ x+2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>1\\ x>-2\end{matrix}\right.\Rightarrow x>1\)
TH2: \(\left\{\begin{matrix} x-1< 0\\ x+2< 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x< 1\\ x< -2\end{matrix}\right.\Rightarrow x< -2\)
Vậy $x\in (1;+\infty)$ hoặc $x\in (-\infty; -2)$
Câu 7:
$|x^2+x-12|=|(x-3)(x+4)|$
Nếu $x\geq 3$ thì $(x-3)(x+4)\geq 0$
$\Rightarrow |x^2+x-12|=x^2+x-12$
BPT trở thành: $x^2+x-12< x^2+x+12$ (luôn đúng)
Nếu $3> x> -4(1)$ thì $(x-3)(x+4)< 0$
$\Rightarrow |x^2+x-12|=-(x^2+x-12)$
BPT trở thành: $-(x^2+x-12)< x^2+x+12$
$\Leftrightarrow 2(x^2+x)>0\Leftrightarrow x>0$ hoặc $x< -1$
Kết hợp với $(1)$ suy ra $3>x>0$ hoặc $-1> x> -4$
Nếu $x\leq -4$ thì $(x-3)(x+4)\geq 0$
$\Rightarrow |x^2+x-12|=x^2+x-12$
BPT trở thành: $x^2+x-12< x^2+x+12$ (luôn đúng)
Vậy BPT có nghiệm $x\in (+\infty; 0)$ hoặc $x\in (-\infty; -1)$
\(-\dfrac{1}{2}x+6< 0\Leftrightarrow-\dfrac{1}{2}x< -6\Leftrightarrow\cdot\dfrac{1}{2}x>6\Leftrightarrow x>12\)
(sai thì thoi nha)
\(-\dfrac{1}{2}x+6< 0\)
\(\Leftrightarrow-\dfrac{1}{2}x< -6\)
\(\Leftrightarrow x>\left(-6\right):\left(-\dfrac{1}{2}\right)\)
\(\Leftrightarrow x>12\)
--> Chọn A