Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(29^2=21^2+20^2\)
nên đây là tam giác vuông
a: Vì không có cạnh nào khi bình phương lên bằng tổng các bình phương của hai cạnh kia nên tam giác này không vuông
c: Tương tự câu a

a) Ta thấy: 92+122=81+144=225=152
=> Đó là 3 cạnh tam giác vuông
b) Ta thấy: 132=169= 144+25= 122+52
=> Đó là 3 cạnh của tam giác vuông
c) 82=64
52+62=25+36=61
Vì 61 khác 64
=> Đây không phải 3 cạnh của tam giác vuông

a) Ta có 3 – 2 < 6 < 3 + 2 bất đẳng thức này sai nên ba độ dài 2cm, 3cm, 6cm không là ba cạnh của tam giác.
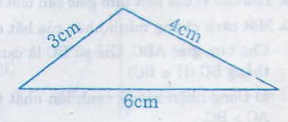
b) Vì 6 = 2 + 4 nên ba độ dài là 2cm, 4cm, 6cm không là 3 cạnh của một tam giác
c) 4 – 3 < 6 < 4 + 3 bất đẳng thức đúng nên ba độ dài 3cm, 4cm, 6cm là 3 cạnh của một tam giác.
a) Nhận xét: 2cm + 3cm = 5cm < 6cm nên bộ ba đoạn thẳng dài 2cm, 3cm, 6cm không phải là bộ ba cạnh của một tam giác.
b) Nhận xét: 2cm + 4cm = 6cm = 6cm nên bộ ba đoạn thẳng dài 2cm, 4cm, 6cm không phải là bộ ba cạnh của một tam giác.
c) Nhận xét: 3cm + 4cm = 7cm > 6cm nên bộ ba đoạn thẳng dài 3cm, 4cm, 6cm là bộ ba cạnh của một tam giác.


a) ta có \(9^2+12^2=81+144=225=15^2\)
vậy tam giác có độ dài 3 cạnh lần lượt là 9 cm, 15 cm, 12 cm là tam giác vuông
b) ta có \(5^2+12^2=25+144=169=13^2\)
vậy tam giác có độ dài 3 cạnh lần lượt là 5 dm, 13 dm, 12 dm là tam giác vuông
c) ta có \(7^2+7^2=49+49=98\\ 10^2=100\) và 98 khác 100
vậy tam giác có độ dài 3 cạnh lần lượt là 7 dm, 7 dm, 10 dm không phải là tam giác vuông

Gọi tam giác đó là \(\Delta\)ABC.AB = 4 cm
AC= 7cm
BC = 8cm
Ta có \(AB^2+AC^2\)=16+49=65 cm
Lại có \(BC^2\)=64
Mà 65\(\ne\)64
\(\Rightarrow\)\(AB^2+AC^2\ne BC^2\)
\(\Delta\)ABC \(K^o\)phải là tam giác vuông (định lí Pi-ta-go) (đpcm)
hok tốt

Nhận xét: Để xét xem một tam giác biết độ dài ba cạnh có phải là tam giác vuông không thì ta xét xem bình phương cạnh lớn nhất có bằng tổng bình phương hai cạnh còn lại không, nếu bằng thì đó là tam giác vuông, nếu không thì bộ ba cạnh đó không lập thành tam giác vuông. (áp dụng định lý đảo của định lý Py – ta – go).