Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

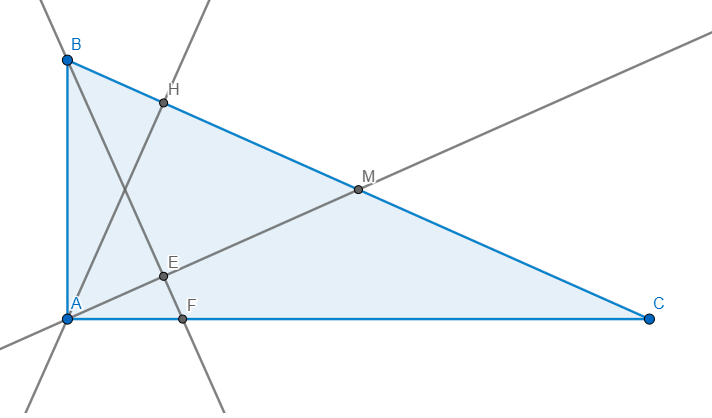
a) Xét Tam giác ABM có hai đường cao AH, BE giao nhau tại D nên D là trực tâm
=> MD cũng là đường cao => MD vuông góc với AB.
b) Tam giác ABF vuông tại A đường cao AE, theo hệ thức lượng trong tam giác vuông:
\(AB^2=BE.BF\)(1)
Tam giác ABC vuông tại A đường cao AH, theo hệ thức lượng trong tam giác vuông:
\(AB^2=BH.BC\)(2)
Từ (1) và (2) suy ra BE.BE=BH.BC(đpcm)

a: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến ứng với cạnh huyền BC
nên BC=2AM
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AB^2=BH\cdot BC\)
hay \(AB^2=2\cdot BH\cdot AM\)

2/ \(\frac{sin^3a-cos^3a}{sin^3a+cos^3a}=\frac{tan^3a-1}{tan^3a+1}=\frac{3^3-1}{3^3+1}=\frac{13}{14}\) (chia tử mẫu cho cos3a)

a) tam giác ABC vuông tại A có AM là trung tuyến \(\Rightarrow AM=\dfrac{BC}{2}\)
Ta có: \(2BH.AM=BH.2AM=BH.BC=AB^2\)
b) tam giác BAF vuông tại A có đường cao AE
\(\Rightarrow BE.BF=BA^2=BH.BC\)
Ta có: \(AM=\dfrac{BC}{2}=BM\Rightarrow\Delta ABM\) cân tại M
\(\Rightarrow\angle MAB=\angle MBA\) mà \(\angle MAB=\angle BFA\Rightarrow\angle ABC=\angle BFA\)
Xét \(\Delta ABF\) và \(\Delta ACB:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle ABC=\angle BFA\end{matrix}\right.\)
\(\Rightarrow\Delta ABF\sim\Delta ACB\left(g-g\right)\Rightarrow\dfrac{AB}{AC}=\dfrac{AF}{AB}\Rightarrow AB^2=AF.AC\)
\(\Rightarrow BE.BF=BH.BC=AF.AC\)