Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

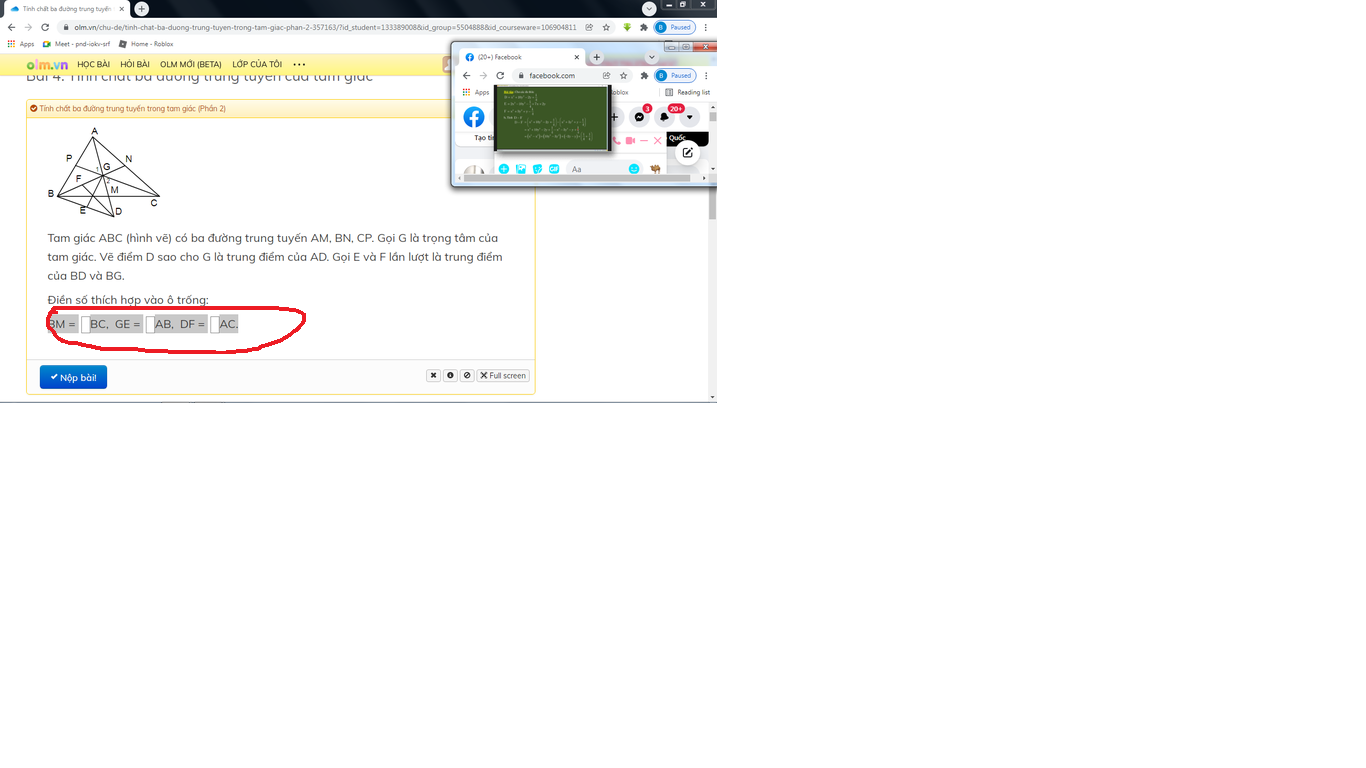
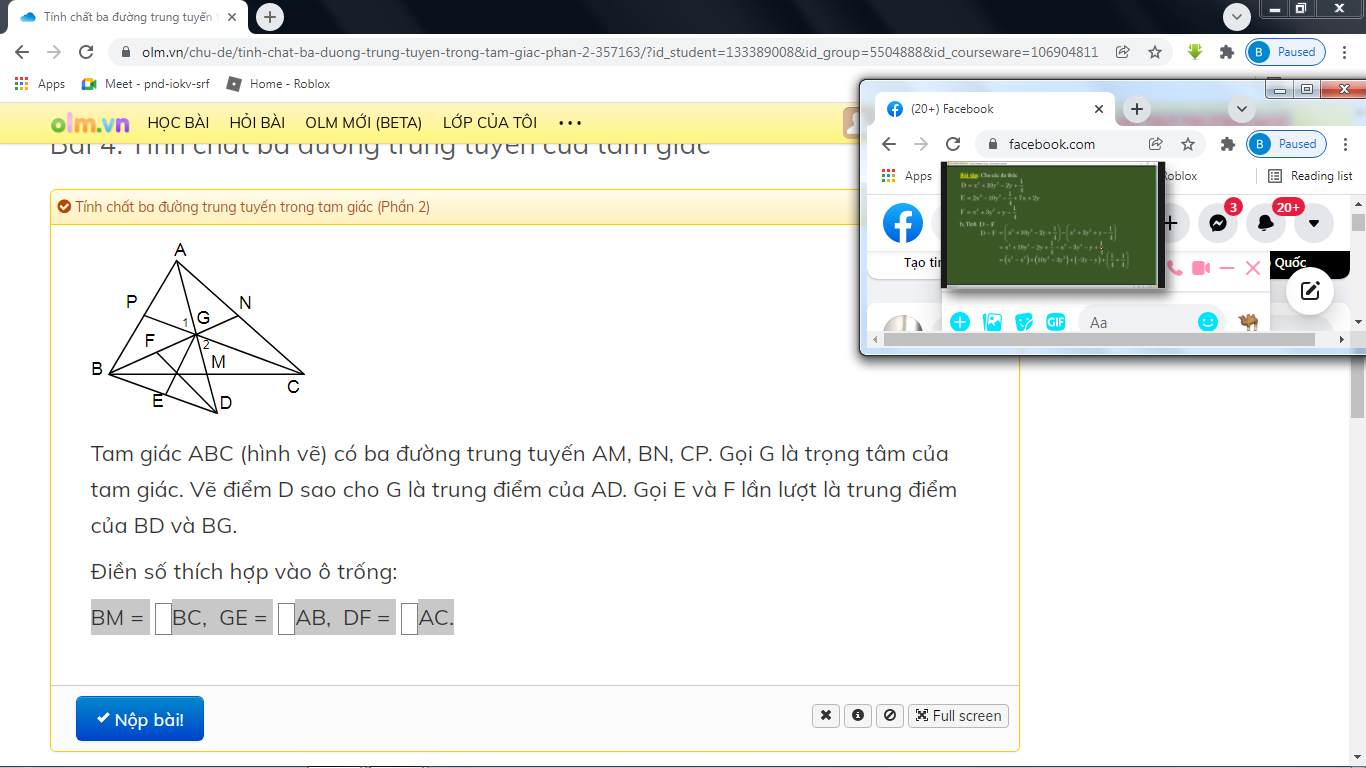
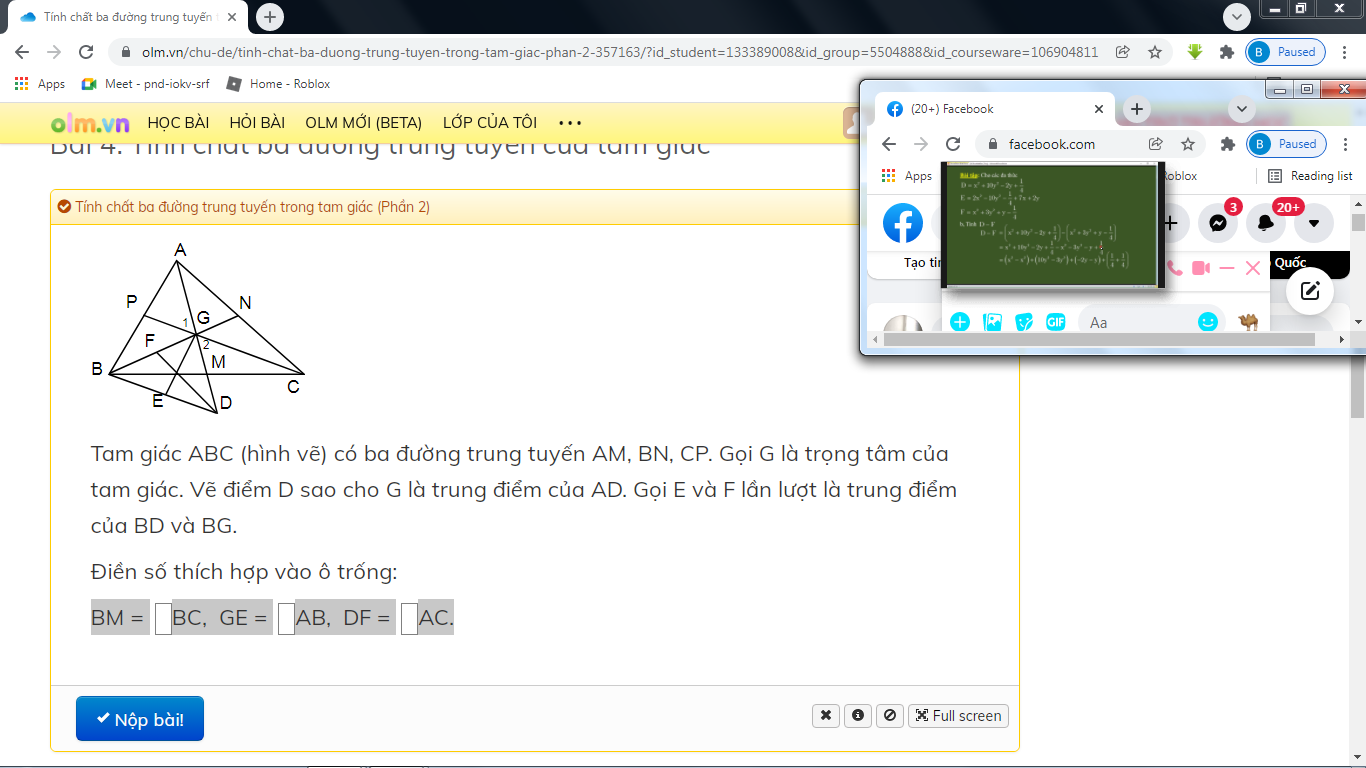
a) Do G là trọng tâm tam giác ABC nên AG = 2GM. Lại có AG = GD nên GD = 2GM hay GM = DM.
Xét tam giác DMB và tam giác GMC có:
DM = GM
BM = CM
\(\widehat{DMB}=\widehat{GMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta DMB=\Delta GMC\left(c-g-c\right)\)
\(\Rightarrow BD=CG\)
b) Do \(\Delta DMB=\Delta GMC\Rightarrow\widehat{FBM}=\widehat{ECM}\)
Xét tam giác FBM và tam giác ECM có:
\(\widehat{FMB}=\widehat{EMC}=90^o\)
BM = CM
\(\widehat{FBM}=\widehat{ECM}\)
\(\Rightarrow\Delta FBM=\Delta ECM\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow BF=CE\left(đpcm\right)\)

Bài 1:
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường trung tuyến
Xét ΔABC có
AH là đường trung tuyến
BD là đường trung tuyến
AH cắt BD tại E
Do đó: E là trọng tâm của ΔABC

a) xét tam giác ADE và tam giác FEC, ta có:
+) AE = EC (E là trung điểm của AC)
+) DE = EF (E là trung điểm của DF)
\(\widehat{ADE}=\widehat{CEF}\)(hai góc đối đỉnh)
=> \(\Delta ADE=\Delta FEC\) (c = g = c)
=> AD = CF (2 cạnh tương ứng)
mà AD = DB (D là trung điểm của AB)
nên: CF = BD
b) ta có:
\(\widehat{EAD}=\widehat{ECF}\left(\Delta ADE=\Delta FEC\right)\)
mà góc EAD và góc ECF nằm so le
nên AD//CF hay AB//CF
xét tam giác BDC và tam giác DCF, ta có:
BD = CF (Cm a)
DC = DC
\(\widehat{BDC}=\widehat{FCD}\)(2 góc so le trong và AB//CF)
=> \(\Delta BDC=\Delta DCF\)(c = g = c)
c) ta có:
\(DE=\frac{1}{2}DF\)(E là trung điểm DF)
DF = BC \(\left(\Delta FCD=\Delta BDC\right)\)
=> \(DE=\frac{1}{2}BC\)