Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A.
Gọi số cần tìm là \(\overline{abc}\) theo đề bài
\(\overline{abc}=100a+10b+c=98a+7b+2a+3b+c=\)
\(=\left(98a+7b\right)+2\left(a+b+c\right)+\left(b-c\right)⋮7\)
\(\Rightarrow\left(98a+7b\right)+2.14+b-c⋮7\)
Ta có \(\left(98a+7b\right)+2.14⋮7\Rightarrow b-c⋮7\) Ta có các trường hợp sau
+Nếu b=c => a=14-(b+c) mà a<=9 => 14-(b+c)<=9 => b+c>=5, mặt khác a>0 => 14-(b+c)>0=> b+c<14 từ đây ta có các trường hợp
b=c=3 => a=8
b=c=4 => a=6
b=c=5 => a=4
b=c=6 => a=2
+ Nếu b khác c
Nếu b=9 => c=2 => a=14-9-2=3
Nếu b=8 => c=1 => a=14-8-1=5
Nếu b=7 => c=0 => a=14-7=7
Nếu c=9 => b=2 => a=14-9-2=3
Nếu c=8 => b=1 => a=14-8-1=5
Nếu c=7 => b=0 => a=14-7=7
\(\Rightarrow\overline{abc}=\left\{833;644,455,266,329,392,518,581,707,770\right\}\)

a: Đúng
Vì ΔABC=ΔDEF
nên AB=DE; BC=EF; AC=DF
=>CABC=CDEF
c: Đúng vì ΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^0\)
d: Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Leftrightarrow3\cdot\widehat{B}=180^0-60^0=120^0\)
\(\Leftrightarrow\widehat{B}=40^0\)
=>\(\widehat{A}=80^0\)(đúng)

2, Theo bài ra ta có : ^A = 600 ; ^B = 2.^C (*)
^A + ^B + ^C = 1800 ( tổng 3 góc trong tam giác ) (**)
Lấy (*) thay vào (**) ta được : ^A + 2.^C + ^C = 1800
<=> 600 + 3.^C = 1800 <=> 3.^C = 1200
<=> ^C = 400 ; => ^B = 2.400 = 800

a: góc ABC+góc ACB=130 dộ
b: Xét ΔOMB vuông tại M và ΔONB vuông tại N có
BO chung
gócMBO=góc NBO
=>ΔOMB=ΔONB
=>OM=ON

a) ta có BIC=180-IBC-ICB=180-1/2B-1/2C
=180-1/2(B+C)=180-1/2.(80+40)=180-1/2.120=180-60=120
vậy BIC=120 độ
b) ta chứng minh tương tự như trên
BIC=180-1/2(B+C)=180-1/2(180-A)=180-1/2.100
=180-50=130
vậy BIC =130

đề sai rồi bạn. Có điểm B rồi làm sao lấy thêm điểm B trên AC nữa?
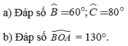
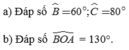
A nhó
A. góc A bằng 40*; góc B bằng 60*; góc C bằng 80*