Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{1}{32}\)
\(\Rightarrow A\approx92^0\)
\(p=\dfrac{AB+AC+BC}{2}=\dfrac{31}{2}\)
\(S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\simeq40\)
\(r=\dfrac{S}{p}=\dfrac{80}{31}\)

Tọa độ C là nghiệm \(\left\{{}\begin{matrix}x+2y-17=0\\4x+3y-28=0\end{matrix}\right.\) \(\Rightarrow C\left(1;8\right)\)
Đường thẳng BC nhận (1;2) là vtpt đường thẳng CK nhận (4;3) là vtpt
Do B thuộc BC, gọi tọa độ B có dạng: \(B\left(-2b+17;b\right)\Rightarrow\overrightarrow{BM}=\left(2b-16;6-b\right)\)
\(\Rightarrow\) Đường thẳng BM nhận \(\left(b-6;2b-16\right)\) là 1 vtpt
Do tam giác cân tại A \(\Rightarrow\widehat{MBC}=\widehat{KCB}\)
\(\Rightarrow\dfrac{\left|1.4+2.3\right|}{\sqrt{1^2+2^2}\sqrt{4^2+3^2}}=\dfrac{\left|1\left(b-6\right)+2\left(2b-16\right)\right|}{\sqrt{1^2+2^2}.\sqrt{\left(b-6\right)^2+\left(2b-16\right)^2}}\)
\(\Leftrightarrow2=\dfrac{\left|5b-38\right|}{\sqrt{5b^2-76b+292}}\)
\(\Leftrightarrow4\left(5b^2-76b+292\right)=\left(5b-38\right)^2\)
\(\Leftrightarrow5b^2-76b+276=0\Rightarrow\left[{}\begin{matrix}b=6\\b=\dfrac{46}{5}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}B\left(5;6\right)\\B\left(-\dfrac{7}{5};\dfrac{46}{5}\right)\end{matrix}\right.\)
Trường hợp B(5;6) loại do khi đó \(\overrightarrow{BM}=\left(-1;-2\right)\) cùng phương BC (vô lý)
Gọi N là trung điểm BC \(\Rightarrow N\left(...\right)\)
Đường cao AN qua N và nhận \(\overrightarrow{BC}\) là 1 vtpt \(\Rightarrow\) phương trình AN
Đường thẳng AB qua B và vuông góc CK nên nhận (3;-4) là 1 vtpt \(\Rightarrow\) phương trình AB
\(\Rightarrow\) Tọa độ A là giao điểm AN và AB
Tính độ dài AN và BC \(\Rightarrow\) diện tích tam giác

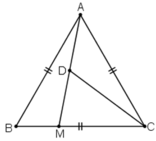
a) Do tam giác ABC là tam giác đều nên 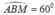 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
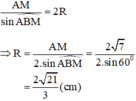
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
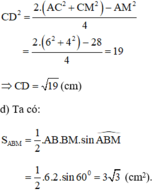

H là trực tâm của tam giác nhỉ.
A có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}2x-y+2=0\\x-2y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\Rightarrow A\left(-1;0\right)\)
B có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}2x-y+2=0\\x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\Rightarrow B\left(0;2\right)\)
H có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}x-2y+1=0\\x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\end{matrix}\right.\Rightarrow H\left(0;\dfrac{1}{2}\right)\)
Phương trình đường thẳng AC: \(y=0\)
Phương trình đường thẳng CH: \(x+2y-1=0\)
C có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}y=0\\x+2y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\Rightarrow H\left(1;0\right)\)