Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
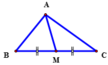
Áp dụng hệ thức đường trung tuyến ![]() ta được:
ta được:
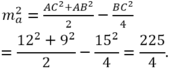
Suy ra : ma= 7,5.

Xét tam giác ABC có đường cao BH:
cos ABC = \(\dfrac{7^2+15^2-13^2}{2\cdot7\cdot15}\) = \(\dfrac{1}{2}\) \(\Rightarrow\) \(\widehat{ABC}=60^o\)
\(p=\dfrac{13+7+15}{2}=17,5\) (cm)
Hê-rông: \(S=\sqrt{17,5\cdot\left(17,5-13\right)\cdot\left(17,5-7\right)\cdot\left(17,5-15\right)}\approx45,5\) (cm2)
\(S=\dfrac{abc}{4R}\) \(\Rightarrow\) \(R=\dfrac{abc}{4S}\approx\dfrac{13\cdot7\cdot15}{4\cdot45,5}=7,5\) (cm)
\(S=\dfrac{1}{2}BH\cdot AC\) \(\Rightarrow\) \(BH=\dfrac{2S}{AC}\approx\dfrac{2\cdot45,5}{13}=7\) (cm)
Chúc bn học tốt!

c: \(AM^2=\dfrac{2\cdot\left(AB^2+AC^2\right)-BC^2}{4}=\dfrac{2\cdot\left(48^2+14^2\right)-50^2}{4}=625\)
nên AM=25(cm)
a: Xét ΔAHB vuông tại H có
\(AB^2=AH^2+HB^2\)
nên AH=16(cm)
Xét ΔAHC vuông tại H và ΔBKC vuông tại K có
\(\widehat{C}\) chung
Do đó: ΔAHC\(\sim\)ΔBKC
Suy ra: \(\dfrac{AH}{BK}=\dfrac{HC}{KC}=\dfrac{AC}{BC}\)
=>16/BK=20/24=5/6
=>BK=19,2(cm)

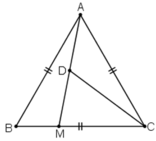
a) Do tam giác ABC là tam giác đều nên 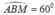 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
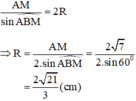
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
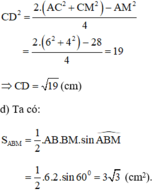

Chọn A.
+ Vì M là trung điểm của BC nên ![]()
Suy ra ![]()
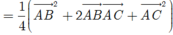
Theo câu trên ta có ![]() nên
nên
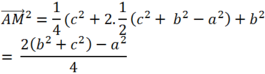

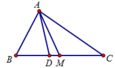
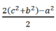
Áp dụng hệ thức đường trung tuyến m a 2 = b 2 + c 2 2 − a 2 4 ta được:
m a 2 = A C 2 + A B 2 2 − B C 2 4 = 12 2 + 9 2 2 − 15 2 4 = 225 4 .
⇒ m a = 15 2 .
Chọn A.