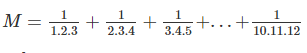Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B114:
a) điền số thích hợp và chỗ trống:
\(\sqrt{1}=....\)
\(\sqrt{1+2+1}=....\)
\(\sqrt{1+2+3+2+1}=.....\)
b) viết tiếp 3 đẳng thức nữa vào danh sách trên.
B115: Cho x là một số hữu tỉ khác 0, y là 1 số vô tỉ. Chứng tỏ x+y và x.y là số vô tỉ.
B116: Biết a là số vô tỉ. Hỏi b là số hữu tỉ hay vô tỉ, nếu:
a, a+b là số hữu tỉ
b, a.b là số hữu tỉ.
B117:Điền các dấu \(\in,\notin,\subset\)thích hợp vào ô vuông:
-2 ... Q
\(-3\frac{1}{5}....Z\)
1 .... R
\(\sqrt{9}....N\)
\(\sqrt{2}...I\)
N ... R
B118:so sánh các số thực:
a) 2,(15) và 2,(14)
b) -0,2673 và -0,267(3)
c) 1,(2357) và 1,2357
d) 0,(428571) và \(\frac{3}{7}\)

Bài 114 : Áp dụng tính chất chia hết , xem xét mỗi tổng ( hiệu ) sau có chia hết cho 6 không ?
a ) 42 + 54
b) 600 - 14
c) 120 + 48 + 20
d) 60 + 15 + 3
Bài 115 : Cho tổng A = 12 + 15 + 21 + x với x ϵ N . Tìm điều kiện của x để A chia hết cho 3 , để A không chia hết cho 3 .
Bài 116 : Khi chia số tự nhiên a cho 24 , ta được số dư là 10 . Hỏi số a có chia hết cho 2 không ? có chia hết cho 4 không ?
Bài 117 : Điền dấu "x" vào ô thích hợp : ( bạn kẻ bảng ra nhé )
Câu : Nếu mỗi số hạng của tổng không chia hết cho 4 thì tổng không chia hết cho 4 Đúng.... Sai.....
Câu : Nếu tổng của hai số chia hết cho 3 , một trong hai số đó chia hết cho 3 thì số còn lại chia hết cho 3 Đúng... Sai...
Bài 118 : Chứng tỏ rằng :
a ) Trong hai số tự nhiên liên tiếp , có một số chia hết cho 2
b) Trong ba số tự nhiên liên tiếp , có một số chia hết cho 3

bn nào cho mk bài tập trong sách bài tập toán 6 tiết 10 nhé


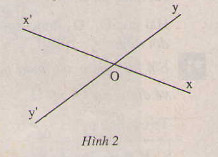
a) Góc xOy và góc ... là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là ... của cạnh Oy'.
b) Góc x'Oy và góc xOy' là ... vì cạnh Ox là tia đối của cạnh ... và cạnh ...
Hướng dẫn giải:
a) Góc xOy và góc x'Oy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'.
b) Góc x'Oy và góc xOy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy' là tia đối của cạnh Oy

\(2M=\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+\frac{5-3}{3.4.5}+...+\frac{12-10}{10.11.12}=\)
\(=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{10.11}-\frac{1}{11.12}=\frac{1}{2}-\frac{1}{11.12}\)
\(\Rightarrow M=\frac{1}{4}-\frac{1}{11.24}=\frac{66-1}{11.24}=\frac{65}{11.24}\)