Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa): a b 3 + a...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

18 tháng 10 2019

Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa): a b 3 + a b 4

#Toán lớp 9

Cao Minh Tâm

18 tháng 10 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

6 tháng 12 2017

Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa): a + a b a + b

#Toán lớp 9

Cao Minh Tâm

6 tháng 12 2017

Cách khác Để học tốt Toán 9 | Giải bài tập Toán 9

Đúng(0)

Pham Trong Bach

4 tháng 7 2017

Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa):

a ) 18 2 - 3 2 b ) a b 1 + 1 a 2 b 2 c ) a b 3 + a b 4 d ) a + a b a + b

#Toán lớp 9

Cao Minh Tâm

4 tháng 7 2017

Để học tốt Toán 9 | Giải bài tập Toán 9

Cách khác:

Để học tốt Toán 9 | Giải bài tập Toán 9

Đúng(0)

Vy Trần

14 tháng 9 2015 - olm

Rút gọn biểu thức sau (giả thiết các biểu thức đều có nghĩa)

\(\sqrt{\frac{a}{b^3}+\frac{a}{b^4}}\)

#Toán lớp 9

Pham Trong Bach

29 tháng 3 2019

Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa): a b 1 + 1 a 2 b 2

#Toán lớp 9

Cao Minh Tâm

29 tháng 3 2019

Đúng(0)

Pham Trong Bach

9 tháng 2 2017

Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa): 18 2 - 3 2

#Toán lớp 9

Cao Minh Tâm

9 tháng 2 2017

Đúng(0)

Trần Tuấn Anh

29 tháng 7 2015 - olm

rút gọn biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa): \(\frac{a+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}\)

#Toán lớp 9

Mr Lazy

29 tháng 7 2015

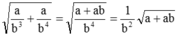
\(=\frac{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}=\sqrt{a}\)

Đúng(0)

Online IOE Việt

6 tháng 9 2017

\(\frac{a+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}=\frac{\left(a+\sqrt{ab}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}=\frac{\left(a+\sqrt{ab}\right)\left(\sqrt{a}-\sqrt{b}\right)}{a-b}\)

Đúng(0)

tamanh nguyen

9 tháng 11 2021

rút gọn các biểu thức sau: (giả thiết các biểu thức chữ đều có nghĩa)

a) \(\dfrac{a-\sqrt{a}}{1-\sqrt{a}}\)

b) \(\dfrac{p-2\sqrt{p}}{\sqrt{p}-2}\)

làm chi tiết hộ em ạ

#Toán lớp 9

Nguyễn Hoàng Minh

9 tháng 11 2021

\(a,=\dfrac{-\sqrt{a}\left(1-\sqrt{a}\right)}{1-\sqrt{a}}=-\sqrt{a}\\ b,=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)

Đúng(0)

Nguyễn Lê Phước Thịnh

9 tháng 11 2021

a: \(=-\sqrt{a}\)

b: \(=\sqrt{p}\)

Đúng(0)

Nguyễn Đức Tố Trân

14 tháng 9 2015 - olm

rút gọn biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa) \(\frac{a+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}\)

#Toán lớp 9

KAl(SO4)2·12H2O

17 tháng 11 2017 - olm

Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa):

a, \(ab\sqrt{1+\frac{1}{a^2b^2}}\)

c, \(\sqrt{\frac{a}{b^3}+\frac{a}{b^4}}\)

#Toán lớp 9

Nguyễn Anh Quân

17 tháng 11 2017

a, = \(\sqrt{a^2b^2.\left(1+\frac{1}{a^2b^2}\right)}\) = \(\sqrt{a^2b^2+1}\)

c, = \(\sqrt{\frac{a+ab}{b^4}}\) = \(\frac{\sqrt{a+ab}}{b^2}\)

k mk nha

Đúng(0)

KAl(SO4)2·12H2O

17 tháng 11 2017

a, \(ab\sqrt{1+\frac{1}{a^2b^2}}\)

\(ab\sqrt{1+\frac{1}{a^2b^2}}=ab\sqrt{\frac{1+a^2b^2}{a^2b^2}}=\frac{ab}{\left|ab\right|}\sqrt{1+a^2b^2}\)

\(=\hept{\begin{cases}\sqrt{1+a^2b^2}ĐK:ab>0\\-\sqrt{1+a^2b^2}ĐKab< 0\end{cases}}\)

b, \(\sqrt{\frac{a}{b^3}+\frac{a}{b^4}}\)

\(\sqrt{\frac{a}{b^3}+\frac{a}{b^4}}=\sqrt{\frac{a+ab}{b^4}}=\frac{1}{b^2}\sqrt{a+ab}\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP