
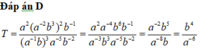
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

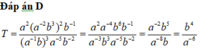

Ta có:
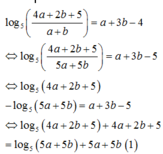
Xét hàm số
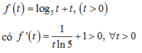
Hàm số f t đồng biến trên 0 ; + ∞
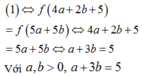
ta có:
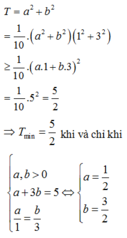
Chọn: D

Đáp án B
Ta có: log 5 4 a + 2 b + 5 a + b = a + 3 b − 4
⇔ log 5 4 a + 2 b + 5 + 4 a + 2 b + 5 = log 5 5 a + 5 b + 5 a + 5 b
Xét hàm số f t = log 5 t + t t > 0 ⇒ f t đồng biến trên 0 ; + ∞
Do đó f 4 a + 2 b + 5 = f 5 a + 5 b ⇔ 4 a + 2 b + 5 = 5 a + 5 b
⇔ a + 3 b = 5 ⇒ T = 5 − 3 b 2 + b 2 = 10 b 2 − 30 b + 25 = 10 b − 3 2 2 + 5 2 ≥ 5 2

Có ABCD là hình bình hành nên A D ⇀ = B C ⇀ = - 1 ; 3 ; 7 ⇒ D 0 ; 5 ; 10
Chọn đáp án C.

Thay a,b,c lần lượt vào biểu thức...
Tính được kết quả:
a) A= \(-\frac{7}{10}\)
b) B= \(-\frac{2}{7}\)
c) C= 0

a) Ta có:
\(A=\left(a-4\right)\left(a+5\right)-\left(a-5\right)\left(a+4\right)\)
\(=\left[\left(a-4\right)a+5\left(a-4\right)\right]-\left[\left(a-5\right)a+4\left(a-5\right)\right]\)
\(=\left[a^2-4a+5a-20\right]-\left[a^2-5a+4a-20\right]\)
\(=a^2-4a+5a-20-a^2+5a-4a+20\)
\(=\left(a^2-a^2\right)+\left(-4a+5a+5a-4a\right)+\left(-20+20\right)\)
\(=0+2a+0\)
\(=2a\)
b) Ta có:
\(B=\left(2-a\right)\left(a+7\right)-\left(a-1\right)\left(a+2\right)\)
\(=\left[\left(2-a\right)a+7\left(2-a\right)\right]-\left[\left(a-1\right)a+2\left(a-1\right)\right]\)
\(=\left[2a-a^2+14-7a\right]-\left[a^2-a+2a-2\right]\)
\(=2a-a^2+14-7a-a^2+a-2a+2\)
\(=\left(2a-7a+a-2a\right)-\left(a^2+a^2\right)+\left(14+2\right)\)
\(=-6a-2a^2+16\)

Đáp án B
Đặt t = 2 − x + 2 + x ⇔ t 2 = 4 + 2 4 − x 2 ⇔ 4 − x 2 = t 2 − 4 2 và x ∈ − 2 ; 2 ⇒ t ∈ 2 ; 2 2
Khi đó, phương trình đã cho trở thành: t − t 2 − 4 2 = m ⇔ 2 m = − t 2 + 2 t + 4 = f t .
Xét hàm số f t = − t 2 + 3 t + 4 trên đoạn 2 ; 2 2 ⇒ min 2 ; 2 2 f t = − 4 + 4 2 ; m a x 2 ; 2 2 f t = 4
Do đó, để phương trình f t = 2 m có nghiệm ⇔ − 2 + 2 2 ≤ m ≤ 2 ⇒ a = − 2 + 2 2 b = 2
Vậy T = a + 2 2 + b − 2 + 2 2 + 2 2 + 2 = 6