Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo cái này nhé e
nguồn Cho đường tròn (O). Từ điểm M nằm ngoài (O) vẽ tiếp tuyến MD, MC với (O) (C, D là các tiếp điểm). Vẽ cát tuyến MAB không đi qua tâm O, A nằm giữa M và B. Tia phân giác góc ACB cắt AB ở E. a) Chứng minh MC = ME. b) Chứng minh DE là tia phân giác góc ADB - Toán học Lớp 9 - Bài tập Toán học Lớp 9 - Giải bài tập Toán học Lớp 9 | Lazi.vn - Cộng đồng Tri thức & Giáo dục

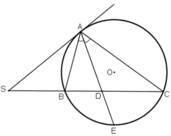
Tia phân giác AD cắt (O) tại E.
+  là góc có đỉnh nằm bên trong đường tròn
là góc có đỉnh nằm bên trong đường tròn
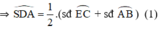
+ 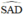 là góc tạo bởi tiếp tuyến AS và dây AE
là góc tạo bởi tiếp tuyến AS và dây AE
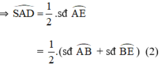
+ 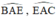 lần lượt là các góc nội tiếp chắn các cung
lần lượt là các góc nội tiếp chắn các cung 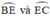
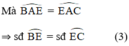
Từ (1); (2) và (3) suy ra 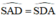
⇒ ΔSAD cân tại S
⇒ SA = SD.

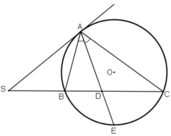
Tia phân giác AD cắt (O) tại E.
+  là góc có đỉnh nằm bên trong đường tròn
là góc có đỉnh nằm bên trong đường tròn
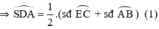
+ 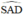 là góc tạo bởi tiếp tuyến AS và dây AE
là góc tạo bởi tiếp tuyến AS và dây AE
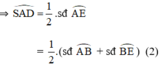
+ 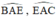 lần lượt là các góc nội tiếp chắn các cung
lần lượt là các góc nội tiếp chắn các cung 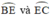
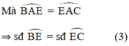
Từ (1); (2) và (3) suy ra 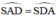
⇒ ΔSAD cân tại S
⇒ SA = SD.
Kiến thức áp dụng
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn.
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

a: góc ABH=góc ABM=1/2*sđ cung BM
góc AEB=1/2(sđ cung BC+sđ cung DM)
=1/2(sđ cung BC+sđ cung MC)
=1/2*sđ cung BM
=>góc AEB=góc ABE
=>ΔABE cân tại A
mà AH là phân giác
nên AH vuông góc với BE
b: Xét ΔMDE và ΔMBD có
góc MDE=góc MBD
góc DME chung
Do đó: ΔMDE đồng dạng với ΔMBD
=>MD/MB=ME/MD
=>MD^2=MB*ME

a: góc AEB=(sd cung BC+sđ cung DM)/2
=1/2(sđ cung BC+sđ cung CM)
=1/2*sđ cung BM
=góc ABM
=góc ABE
=>ΔABE cân tại A
mà AH là phân giác
nen AH vuông góc với BE
b: Xét ΔMDE và ΔMBD có
góc MDE=góc MBD
góc DME chung
=>ΔMDE đồng dạng với ΔMBD
=>MD/MB=ME/MD
=>MD^2=MB*ME
tiếp tuyến AB và cát tuyến MAB là sao bạn ?