Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

HD: Số tiền cả gốc lẫn lãi của người đó sau n năm là: T = 100(1 + 6%)n
Để số tiền nhiều hơn 300 triệu thì:
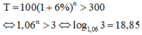
Vậy sau ít nhất 19 năm người đó nhận được số tiền nhiều hơn 300 triệu. Chọn A.

Đáp án B
Gọi A là số tiền gốc ban đầu, lãi suất r/năm, số tiền gửi thêm là a (triệu đồng)
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận đc là A(1+r)
Sau năm thứ 2, cả gốc và lãi ông nhận được là
![]()
Sau năm thứ 3, cả gốc và lãi ông nhận được:
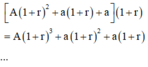
Sau năm thứ n, ông Minh nhận được số tiền:
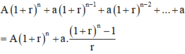
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
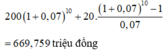

Đáp án C
Gọi A là số tiền gốc ban đầu, lãi suất r / năm, số tiền gửi thêm là a (triệu đồng).
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận được là: A 1 + r
Sau năm thứ 2, cả gốc và lãi ông nhận được là: A 1 + r + a 1 + r = A 1 + r 2 + a 1 + r
Sau năm thứ 3, cả gốc và lãi ông nhận được:
A 1 + r 2 + a 1 + r + a 1 + r = A 1 + r 3 + a 1 + r 2 + a 1 + r
…
Sau năm thứ n, ông Minh nhận được số tiền:
A 1 + r n + a 1 + r n − 1 + a 1 + r n − 2 + . .. + a = A 1 + r n + a . 1 + r n − 1 r
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
200 1 + 0 , 07 10 + 20. 1 + 0 , 07 10 − 1 0 , 07 = 669 , 759 triệu đồng.

Đáp án C
Áp dụng công thức lãi kép: A n = A 1 + r n
Với A n , y M ' = là số tiền nhận được sau n năm (cả gốc và lãi).
A là tiền gốc.
n là số năm gửi.
r là lãi suất hằng năm.
Cách giải:
Sau n năm người đó nhận được A n = 75 1 + 5,4 100 n > 100 ⇔ n > 5,47
Vậy sau ít nhất 6 năm người đó nhận được số tiền nhiều hơn 100 triệu đồng.

Đáp án A
Số tiền lãi người này nhận được sau 5 năm là
50 ( 1 + 0 , 07 ) 5 - 50 ≈ 20 , 128 (triệu đồng).


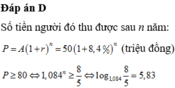
Sau 18 năm số tiền ông Chính nhận được cả gốc lẫn lãi là:
(triệu đồng).
Chọn C