Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một người gửi tiết kiệm vào ngân hàng với lãi suất 7,5%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và lãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không rút tiền ra?
Bốn phương án trả lời là: A 12 năm; B 10 năm; C 9 năm; D 11 năm.
# HOK TỐT #

Đây là bài toán lãi kép gửi một lần có công thức :
T=M.\(\left(r+1\right)^n\) trong đó :T:số tiền cả vốn lẫn lãi sau n kì hạn
M :số tiền gửi ban đầu
n:số kì hạn tính lãi
r:lãi suất định kì
như vậy ta có :
250 =100.\(\left(1+7\%\right)^n\)
\(\Leftrightarrow1,07^n\)=2,5 \(\Leftrightarrow\)n=\(\log\left(2,5\right)_{1,07}\) =13,54 vậy là đáp án B sau 13 năm

Đáp án C
Phương pháp:
Công thức lãi kép, không kỳ hạn: An = M(1 + r%)n
Với: An là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%).
Cách giải:
Số tiền ông A rút ra sau 5 năm đầu là: 100.1 + 8%5 ≈ 146,933 (triệu đồng)
Số tiền ông A tiếp tục gửi là: 146,933:2 ≈ 73,466 (triệu đồng)
Số tiền ông A nhận được sau 5 năm còn lại là: 73,466.1 + 8%5 ≈ 107,946 (triệu đồng)
Sau 10 năm ông A đã thu được số tiền lãi là: 107,946 - 73,466 + 146,933-100 ≈ 81,412 (triệu đồng)

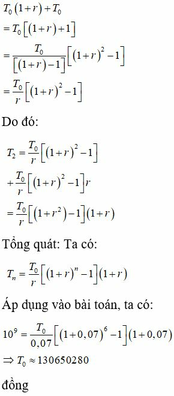
Số tiền cả gốc lẫn lãi ông B nhận được sau 12 năm là:
Suy ra, số tiền lãi L ông B nhận được sau 12 năm là:
Chọn A