Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
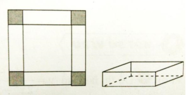
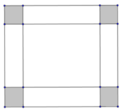
Hình hộp có đáy là hình vuông cạnh: 12 - 2x
Chiều cao của hình hộp là: x
Thể tích hình hộp là y = x ( 12 - 2 x ) 2
Bài toán đưa về tìm x ∈ (0; 6) để hàm số y = f ( x ) = x ( 12 - 2 x ) 2 có giá trị lớn nhất.
y ' = 1 ( 12 - 2 x ) 2 + x . 2 . ( 12 - 2 x ) . ( - 2 )
12 x 2 - 96 x + 144 ;
y' xác định ∀ x ∈ (0; 6)
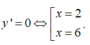
Bảng biến thiên
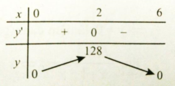
Hàm số đạt giá trị lớn nhất tại x=2

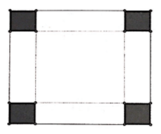
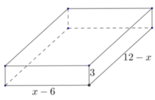
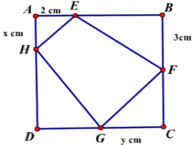
Ta có SEFGH nhỏ nhất ↔ S = S A E H + S C G F + S D G H lớn nhất
Tính được 2S= 2x+ 3y+ (6-x) (6-y) = xy-4x-3y+36 (1)
Mặt khác ∆ AEH đồng dạng ∆CGF nên A E C G = A H C F ⇒ x y = 6
Từ (1) và (2) suy ra 2S = 42 - ( 4 x - 18 x )
Ta có 2S nhỏ nhất khi và chỉ khi 4 x - 18 x nhỏ nhất.
Biểu thức nhỏ nhất 4 x - 18 x nhỏ nhất ↔ 4 x = 18 x ⇒ x = 3 2 2 ⇒ y = 2 2
Vậy x+y = 3 2 2 + 2 2
Chọn D.

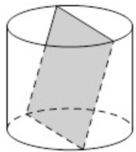
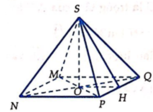
Chọn đáp án B.
Hộp hình trụ có R = h = 10. Gọi a là độ dài cạnh hình vuông (tấm bìa) đã cho. Gọi AB, CD lần lượt là cạnh hình vuông trên mặt đáy; cạnh trên mặt phía trên của hộp. Gọi E, F lần lượt là hình chiếu vuông góc của C, D xuống mặt đáy.
Ta có: E F = C D = A B E F / / C D / / A B
⇒ A E F B là hình chữ nhật nội tiếp đường tròn có bán kính R = 10 .
Do đó A B 2 + B F 2 = A F 2
⇔ A B 2 + B F 2 = 4 R 2 ⇔ a 2 + B F 2 = 4 R 2 ( 1 )
Mặt khác theo pitago có:
B D 2 = B F 2 + F D 2 ⇔ a 2 = B F 2 + h 2 ( 2 )
Từ (1) và (2) có:
4 R 2 - a 2 = a 2 - h 2 ⇔ a 2 = h 2 + 4 R 2 2 = 10 2 + 4 × 10 2 2 = 250





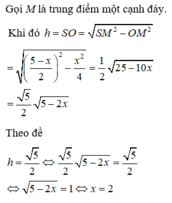
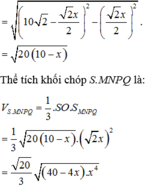
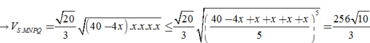
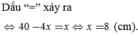
15 cm
Bàn giúp mình giải rồi chụp giúp mình nha