Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phép lật mặt là sự thay đổi chiều hướng của đa giác đó ông, tức là lật ngược lại ý :)

Ôi chết rồi em không để ý, dạo này hoc24 không có phần câu hỏi trùng lặp nên em không biết thầy ạ. Em cảm ơn thầy ạ.

Câu 6: Thử làm phát :v
Bất đẳng thức cần chứng minh tương đương với:
\(1-a-b-c-d+ab+bc+cd+da+ac+bd-abc-bcd-cda-dab+abcd+a+b+c+d\ge1\)
\(\Leftrightarrow ab+bc+cd+da+ac+bd-abc-bcd-cda-dab+abcd\ge0\).
Điều trên luôn đúng do \(a,b,c,d\in\left[0;1\right]\).
(Hy vọng sẽ có cách khác chứ nhân ra ntn nhìn phức tạp quá).
Mong mấy câu Vật Lý ngày mai sẽ khó hơn câu Toán.C8 một chút
a/ Quãng đường từ trường đến Đà Lạt:
\(S=vx=45x\left(km\right)\)
\(\Rightarrow y=3+45x\left(km\right)\)
b/ Từ trường đến Đà Lạt: 318-3= 315(km)
\(\Rightarrow x=\dfrac{315}{45}=7\left(h\right)\)
Thêm thời gian nghỉ 1,5h
\(\Rightarrow t=x+1,5=8,5\left(h\right)\)
\(\Rightarrow15-8,5=6,5\left(h\right)\)
Vậy xe xuất phát từ 6h 30'.
Và bạn An phải đi với vận tốc: \(\dfrac{3}{0,5}=6\left(km/h\right)\)

[Toán.C17_19.1.2021]
Gọi x, y, z là các số nguyên dương thỏa mãn \(a=x+y;b=y+z;c=z+x\)
Khi đó: \(a^2b\left(a-b\right)+b^2c\left(b-c\right)+c^2a\left(c-a\right)\ge0\left(1\right)\)
\(\Leftrightarrow\left(x+y\right)^2\left(y+z\right)\left(x-z\right)+\left(y+z\right)^2\left(z+x\right)\left(y-x\right)+\left(z+x\right)^2\left(x+y\right)\left(z-y\right)\ge0\)
\(\Leftrightarrow x^3z+y^3x+z^3y\ge x^2yz+xy^2z+xyz^2\)
\(\Leftrightarrow\dfrac{x^2}{y}+\dfrac{y^2}{z}+\dfrac{z^2}{x}\ge x+y+z\left(2\right)\)
Áp dụng BĐT BSC:
\(\dfrac{x^2}{y}+\dfrac{y^2}{z}+\dfrac{z^2}{x}\ge\dfrac{\left(x+y+z\right)^2}{x+y+z}=x+y+z\)
\(\Rightarrow\left(2\right)\) đúng \(\Rightarrow\left(1\right)\) đúng
VietNam TST, 1996.
Chuẩn hóa \(x^2+y^2+z^2=1.\) Cần chứng minh:
\(6\left(x+y+z\right)\le27xyz+10\)
Ta có: \(1=x^2+y^2+z^2\ge3\sqrt[3]{x^2y^2z^2}\Rightarrow x^2y^2z^2\le\dfrac{1}{27}\Rightarrow-\dfrac{\sqrt{3}}{9}\le xyz\le\dfrac{\sqrt{3}}{9}\)
Do đó: \(VP\ge27\cdot\left(-\dfrac{\sqrt{3}}{9}\right)+10=10-3\sqrt{3}>0.\)
Nếu $x+y+z<0$ thì $VP>0>VT$ nên ta chỉ xét khi $x+y+z\geq 0.$
Đặt $\sqrt{3}\geq p=x+y+z>0;q=xy+yz+zx,r=xyz.$
Bất đẳng thức cần chứng minh tương đương với:\(6p\le27r+10\quad\left(1\right)\)
Mà \(x^2+y^2+z^2=1\Leftrightarrow p^2-2q=1\Rightarrow q=\dfrac{\left(p^2-1\right)}{2}\quad\left(2\right)\)
Ta có: $$(x-y)^2(y-z)^2(z-x)^2\geq 0.$$
Chuyển sang \(\textit{pqr}\) và kết hợp với $(2)$ suy ra \({\dfrac {5\,{p}^{3}}{54}}-\dfrac{p}{6}-{\dfrac {\sqrt {2 \left(3- {p}^{2} \right) ^{3}}}{54}}\leq r \)
Từ đây thay vào $(1)$ cần chứng minh:
$$\dfrac{5}{2}p^3-\dfrac{21}{2}p+10\geqslant \dfrac{1}{2}\sqrt{2\left(3-p^2\right)^3}$$
Hay là $$\dfrac{1}{4} \left( 27\,{p}^{4}+54\,{p}^{3}-147\,{p}^{2}-148\,p+346 \right) \left( p-1 \right) ^{2}\geqslant 0.$$
Đây là điều hiển nhiên.

[Toán.C23 _ 21.1.2021]
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\)
Giả thiết trở thành \(2x+9y+21z\le12xyz\)
\(\Leftrightarrow3z\ge\dfrac{2x+8y}{4xy-7}\)
Áp dụng BĐT Cosi và BĐT BSC:
Khi đó \(P=x+2y+3z\)
\(\ge x+2y+\dfrac{2x+8y}{4xy-7}\)
\(=x+\dfrac{11}{2x}+\dfrac{1}{2x}\left(4xy-7+\dfrac{4x^2+28}{4xy-7}\right)\)
\(\ge x+\dfrac{11}{2x}+\dfrac{1}{x}\sqrt{4x^2+28}\)
\(=x+\dfrac{11}{2x}+\dfrac{3}{2}\sqrt{\left(1+\dfrac{7}{9}\right)\left(1+\dfrac{7}{x^2}\right)}\)
\(\ge x+\dfrac{11}{2x}+\dfrac{3}{2}\left(1+\dfrac{7}{3x}\right)\)
\(\ge x+\dfrac{9}{x}+\dfrac{3}{2}\ge\dfrac{15}{2}\)
\(\Rightarrow minP=\dfrac{15}{2}\Leftrightarrow a=\dfrac{1}{3};b=\dfrac{4}{5};c=\dfrac{3}{2}\)
Mấy câu có thêm dòng trích từ mấy đề quốc gia, quốc tế gì gì đó đâm ra nản luôn.
C23 cách khác: Điểm rơi \(a=\dfrac{1}{3};b=\dfrac{4}{5};c=\dfrac{3}{2}\) nên ta đặt \(a=\dfrac{1}{3}x;b=\dfrac{4}{5}y;c=\dfrac{3}{2}z\).
Ta có \(21ab+2bc+8ca\le12\Leftrightarrow\dfrac{28}{5}xy+\dfrac{12}{5}yz+4zx\le12\Leftrightarrow7xy+3yz+5zx\le15\).
Áp dụng bất đẳng thức AM - GM: \(15\ge7ab+3bc+5ca\ge15\sqrt[15]{\left(xy\right)^7.\left(yz\right)^3.\left(zx\right)^5}=15\sqrt[15]{x^{12}y^{10}z^8}\)
\(\Rightarrow x^6y^5z^4\le1\);
\(P=\dfrac{1}{a}+\dfrac{2}{b}+\dfrac{3}{c}=3x+\dfrac{5}{2}y+2z=\dfrac{1}{2}\left(\dfrac{6}{x}+\dfrac{5}{y}+\dfrac{4}{z}\right)\ge\dfrac{1}{2}.15\sqrt[15]{\left(\dfrac{1}{x}\right)^6.\left(\dfrac{1}{y}\right)^5.\left(\dfrac{1}{z}\right)^4}=\dfrac{15}{2}.\sqrt[15]{\dfrac{1}{x^6y^5z^4}}\ge\dfrac{15}{2}\).
Đẳng thức xảy ra khi \(x=y=z=1\) tức \(a=\dfrac{1}{3};b=\dfrac{4}{5};c=\dfrac{3}{2}\).Vậy Min P = \(\dfrac{15}{2}\) khi \(a=\dfrac{1}{3};b=\dfrac{4}{5};c=\dfrac{3}{2}\).
P/s: Lời giải nhìn có vẻ đơn giản nhưng muốn tìm điểm rơi thì phải dùng bđt AM - GM suy rộng.

C27.Gọi AB là dây vuông góc với OP tại P , và dây CD là dây bất kỳ đi qua P vàkhông trùng với AB .
Kẻ \(OH\perp CD\)
\(\Delta OHP\) vuông tại H\(\Rightarrow\) OH < OP \(\Rightarrow\) CD > AB
Như vậy trong tất cả các dây đi qua P , dây vuông góc với OP tại P có độ dài nhỏ nhất.

Bài 2.
Ta có:a2+b2+c2+2abc+1≥2(ab+bc+ca)
⇔ (a2-2ab+b2)+(c2-2c+1)+(2c+2abc-2bc-2ca)≥0
⇔ (a-b)2+(c-1)2+2c(a-1)(b-1)≥0
Vì a,b,c≥0 ⇒ 2c(a-1)(b-1)≥0
Dấu "=" xảy ra ⇔ a=b=c=1
C25: b5: Sử dụng kĩ thuật Côsi ngược dấu:
Ta có: \(\dfrac{1}{2bc^2+1}=1-\dfrac{2bc^2}{2bc^2+1}\ge1-\dfrac{2bc^2}{3\sqrt[3]{b^2c^4}}=1-\dfrac{2\sqrt[3]{bc^2}}{3}\)
Cmtt ta được: \(\dfrac{1}{2ca^2+1}\ge1-\dfrac{2\sqrt[3]{ca^2}}{3};\dfrac{1}{2ab^2+1}\ge1-\dfrac{2\sqrt[3]{ab^2}}{3}\)
\(\Rightarrow VT\ge1-\dfrac{2\sqrt[3]{bc^2}}{3}+1-\dfrac{2\sqrt[3]{ca^2}}{3}+1-\dfrac{2\sqrt[3]{ab^2}}{3}=3-2\left(\dfrac{\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}}{3}\right)\)
Ta có: Theo bđt Côsi:
\(\sqrt[3]{bc^2}=\sqrt[3]{b.c.c}\le\dfrac{b+c+c}{3}=\dfrac{b+2c}{3}\)
\(\sqrt[3]{ca^2}=\sqrt[3]{c.a.a}\le\dfrac{c+a+a}{3}=\dfrac{c+2a}{3}\)
\(\sqrt[3]{ab^2}=\sqrt[3]{a.b.b}\le\dfrac{a+b+c}{3}=\dfrac{a+2b}{3}\)
\(\Rightarrow\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}\le\dfrac{b+2c+c+2a+a+2b}{3}=a+b+c=3\)
\(\Rightarrow3-2\left(\dfrac{\sqrt[3]{bc^2}+\sqrt[3]{ca^2}+\sqrt[3]{ab^2}}{3}\right)=1\)
\(\Rightarrow VT\ge1\)
Dấu ''='' xảy ra khi a=b=c=1




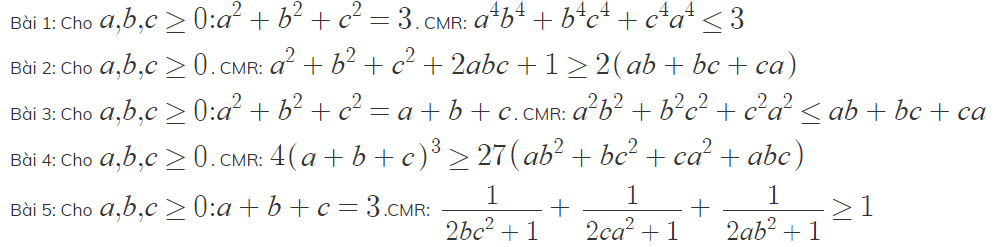
Vì C2 mình gửi nên mình làm câu 3:
Gọi S(n) là tổng tất cả các tích thu được.
Ta chứng minh bằng quy nạp rằng S(n) = -1 với mọi giá trị của n là số tự nhiên khác 0.
Thật vây, ta có S(1) = -1
Giả sử ta đã có S(n) = -1.
Ta cần chứng minh S(n + 1) = -1.
Ta thấy sau khi thêm tập hợp A = {-1; -2;,,,; -n} một phần tử -(n + 1), tập hợp A tăng thêm số tập hợp con bằng số tập hợp con của tập hợp A lúc đầu.
Do đó: \(S\left(n+1\right)-S\left(n\right)=S\left(n\right).\left[-\left(n+1\right)\right]-\left(n+1\right)=n+1-n-1=0\Rightarrow S\left(n+1\right)=S\left(n\right)=-1\).
Vậy ta có đpcm.
Các tập hợp con mới của A thì chính là các tập hợp con của tập hợp A cũ thêm phàn tử -(n + 1) nên ta ra được công thức như trên.