Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.chọn Xo=0 tại vị trí xe bắt đầu cđ.=> ta có Xo=0 ;Vo=0 .=>X=Xo+Vot+1/2at^2<=>X=t^2
b.áp dụng ct V^2-Vo^2=2as => vs Vo=0 =>V= căn 2as => V=10can2
c.---------------------------------------------------- ,AC=1/2AB=25 =>V=căn 2as =>V=10

Tại vị trí gặp nhau của hai xe thì
Xe xuất phát từ A có vận tốc bằng
v 1 = a 1 t = 2,5. 10 - 2 .400 = 10(m/s) = 36(km/h)
Xe xuất phát từ B có vận tốc bằng
v 2 = a 2 t = 2,0. 10 - 2 .400 = 8(m/s) = 28,8(km/h)

Ta có :
\(s_{AB}=\dfrac{1}{2}at^2\Leftrightarrow a=1,4m\backslash s\)
\(v_B^2-v^2_A=2as\)
\(\Leftrightarrow v_A=\sqrt{2as-v^2_B}=18m\backslash s\)
Lại có :
\(v_A^2-v^2_O=2as_{OA}\)
\(\Leftrightarrow OA=\sqrt{\dfrac{v_A^2}{2a}}=10,76m\)
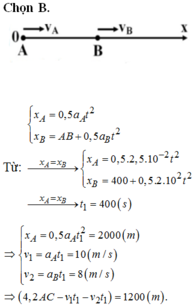
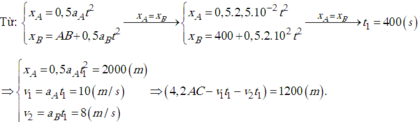
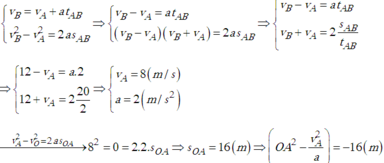
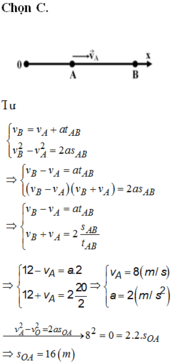
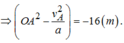
a) Vận tốc của xe khi qua A là :
\(\left\{{}\begin{matrix}v_B=v_A+a.t\\S=v_A.t+\frac{1}{2}a.t^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}12=v_A+a.2\\20=v_A.2+2.a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v_A=8m\text{ /}s\\a=2m\text{ /}s^2\end{matrix}\right.\)
b)Khoảng cách từ nơi xuất phát đến A là :
\(S_{OA}=\frac{v^2_A}{2.a}=\frac{8^2}{2.2}=16m\)
c)Tốc độ trung bình trên các quãng đường AB, OA, OB là :
\(v_{tb_{AB}}=\frac{20}{2}=10m\text{/}s\)
\(v_{tb_{OA}}=\frac{OA}{\frac{v_A}{a}}=\frac{10}{\frac{8}{2}}=2,5m\text{/}s\)
\(v_{tb_{OB}}=\frac{10+20}{4+2}=5m\text{/}s\)