Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(v_{tb}=\dfrac{S_1+S_2+S_3}{t_1+t_2+t_3}=\dfrac{S}{\dfrac{S}{36}+\dfrac{S}{42}+\dfrac{S}{30}}=\dfrac{1260}{107}\left(km/h\right)\)
\(v_{tb}=\dfrac{\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}}{\dfrac{\dfrac{1}{3}}{12}+\dfrac{\dfrac{1}{3}}{14}+\dfrac{\dfrac{1}{3}}{10}}=\dfrac{1260}{107}\approx11,776\left(\dfrac{km}{h}\right)\)

có vẻ hơi thiếu dữ kiện rồi, bạn phải cho quãng đường hoặc thời gian của cả 2 đoạn đường thì mới tính được

Vận tốc trung bình của người đi xe đạp trên đoạn đường AB là :
(14+16+8) : 3 = 12,6666..... (km/giờ) \(\approx\)12,67 (km/giờ)
Vậy vận tốc trung bình của người đi xe đạp trên đoạn đường AB là 12,67 km/giờ

\(=>t1=\dfrac{\dfrac{1}{3}S}{12}=\dfrac{S}{36}\left(h\right)\)
\(=>t2=\dfrac{\dfrac{1}{3}S}{8}=\dfrac{S}{24}\left(h\right)\)
\(=>t3=\dfrac{\dfrac{1}{3}S}{6}=\dfrac{S}{18}\left(h\right)\)
\(=>vtb=\dfrac{S}{t1+t2+t3}=\dfrac{S}{\dfrac{S}{36}+\dfrac{S}{24}+\dfrac{S}{18}}=\dfrac{S}{\dfrac{432S+648S+864S}{15552}}\)
\(=\dfrac{S}{\dfrac{1944S}{15552}}=\dfrac{15552}{1944}=8km/h\)

Tóm tắt:
\(s_1=s_2=s_3=\dfrac{1}{3}s_{AB}\)
\(v_1=13km/h\\ v_2=15km/h\\ v_3=17km/h\)
\(-----\\ v_{TB}=?\)
-- giải ---
Gọi độ dài mỗi đoạn đường là s
Ta có
\(v_{TB}=\dfrac{s+s+s}{t_1+t_2+t_3}=\dfrac{s+s+s}{\dfrac{s}{v_1}+\dfrac{s}{v_2}+\dfrac{s}{v_3}}\\ =\dfrac{3s}{s\left(\dfrac{1}{v_1}+\dfrac{1}{v_2}+\dfrac{1}{v_3}\right)}=\dfrac{3}{\dfrac{1}{v_1}+\dfrac{1}{v_2}+\dfrac{1}{v_3}}\)
Mình gợi ý cách làm. Đến đây thì bạn có thể thế số và bấm máy tính là tìm đc vTB rồi nhé!


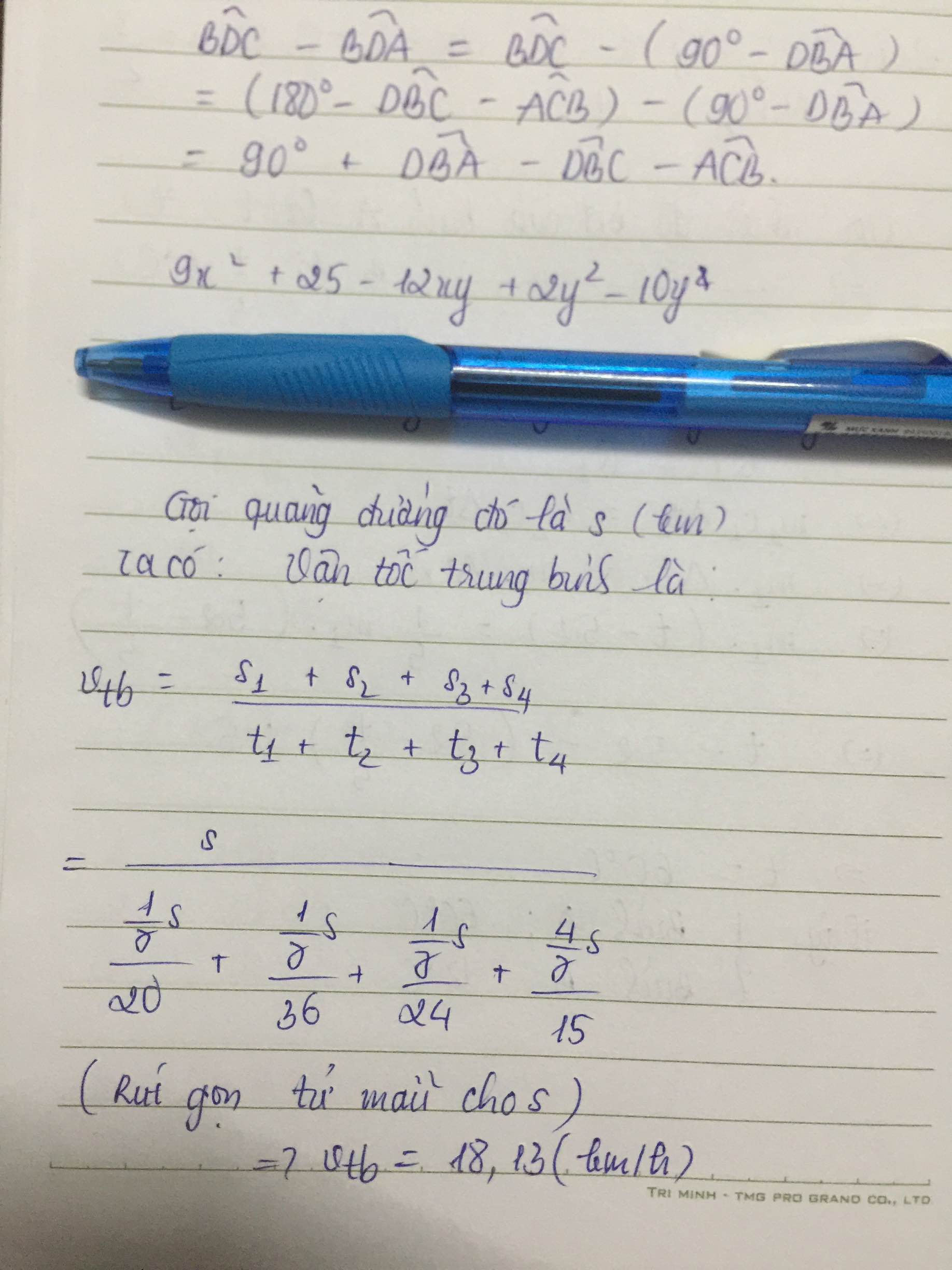
thời gian đi từng đoạn
\(t_1=\dfrac{S}{45}\)
\(t_2=\dfrac{S}{30}\)
\(t_3=\dfrac{S}{24}\)
\(v_{tb}=\dfrac{1}{\dfrac{1}{45}+\dfrac{1}{30}+\dfrac{1}{24}}\approx10,3\left(km/h\right)\)