Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
+ Đoàn tàu có v 0 = 0 ⇒ S = 1 2 a t 2
Gọi ℓ là chiều dài một toa tàu
t 1 là thời gian toa thứ nhất qua người đó
t 14 là thời gian toa thứ 14 qua người đó
t 15 là thời gian toa thứ 15 qua người đó
S 1 = l = 1 2 a t 1 2 1 S 14 = 14 l = 1 2 a t 14 2 2 S 15 = 15 l = 1 2 a t 15 2 3 → 1 ; 2 ; 3 l t 1 2 = 14 l t 14 2 = 15 l t 15 2 4 ⇒ t 14 = 14 t 1 t 15 = 15 t 1
+ Thời gian tao 15 đi qua người ấy là: Δ t = t 15 − t 14 = 15 − 14 t 1 = 0 , 39 s

+ Giả sử chiều dài mỗi toa là L
+ Khi toa 1 qua mặt người ta có: \(L=0,5at^2\Rightarrow t=\sqrt{\frac{2L}{a}}\)
+ Thời gian khi n qua mặt:
\(nL=0,5at^2_n\Rightarrow t_n=\sqrt{\frac{2nL}{a}}\)
+ Thời gian khi (n - 1) toa qua mặt:
\(\left(n-1\right)L=0,5at^2_{n-1}=t_{n-1}=\frac{\sqrt{\left(2n-1\right)L}}{a}\)
Từ những điều trên => thời gian toa thứ n qua mặt là: \(\Delta t=t_n-t_{n-1}\Leftrightarrow\Delta t=t\left(\sqrt{n}-\sqrt{n-1}\right)\)
Chiều dài toa thứ nhất:
\(L=\frac{at^2_1}{2}\Rightarrow t1=\sqrt{\frac{2L}{2}}\left(1\right)\)
Gọi T và + Δt lần lượt là khoảng thời gian từ lúc tàu chuyển động cho tới khi toa thứ n bắt đầu đi qua, và đã đi qua người.
Xem khoảng cách giữa các toa không đáng kể.
Khi đó, quãng đường mà tàu đi được trong thời gian T: \(S1=\frac{aT^2}{2}=\left(n-1\right)L\Rightarrow T=\sqrt{\frac{2\left(n-1\right)L}{a}}\)
Quãng đường tàu đi được torng thời gian ΔT là:\(S2=\frac{a\left(T+\Delta t\right)^2}{2}=n.L\Rightarrow T+\Delta t=\sqrt{\frac{2nL}{a}}\)
\(\Delta t=\sqrt{\frac{2nL}{2}}-\sqrt{\frac{2\left(n-1\right)L}{a}}\)
Thay (1) vào là được đáp số.

Nếu chiều dài mỗi toa là L
=> Khi toa 1 qua mặt người ấy, ta có: \(L=0,5at^2=t=\sqrt{\dfrac{2L}{a}}\)
Thời gian khi qua mặt: \(nL=0,5at^2_n=t_n=\sqrt{\dfrac{2nL}{a}}\)
Thời gian khi n-1 toa qua mặt: \(\left(n-1\right)L=0,5at_{n-1}=t_{n-1}=\sqrt{\dfrac{\left(2n-1\right)L}{a}}\)
=> Thời gian toa thứ n qua mặt: \(\Delta t=t_n-t_{n-1}\Leftrightarrow\Delta t=t\left(\sqrt{n}-\sqrt{n-1}\right)\)
Kết Qủa đúng đãng lễ phải là t\(\sqrt{n}\)-t\(\sqrt{n-1}\) chứ
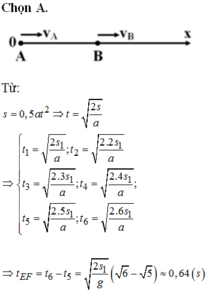
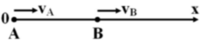
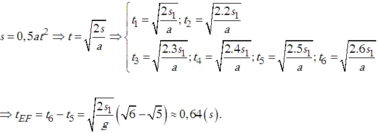
Chọn A.