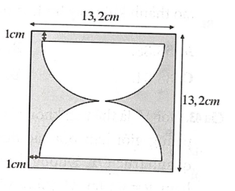
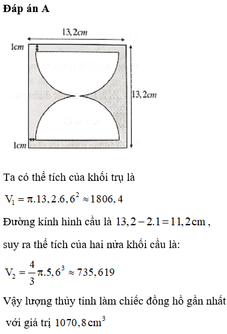
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

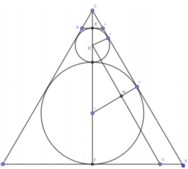
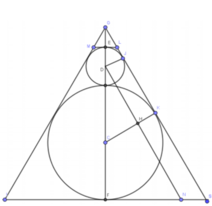
Gọi tâm của hai đường tròn trong (N) là C và D. Ta có GS là tiếp tuyến chung của hai đường tròn tại K và J. Khi đó: D J ⊥ G S C K ⊥ G S
Kẻ D N / / G S ( N ∈ I S ) , khi đó DHKJ là hình chữ nhật nên HK=DJ=1 cm, do đó ta có CH=2 cm.
Ta có ∆ D H C đồng dạng ∆ G J D nên D J C H = G D C D
⇒ D G = D J . C D C H = 1 . 4 2 = 2 cm từ đó suy ra GF = 9 cm.
Ta có ∆ D H C đồng dạng ∆ G F S ⇒ G S D C = G F D H
⇒ G S = D C . G F D H = D C . G F D C 2 - C H 2 = 6 3 cm
⇒ F S = G S 2 - G F 2 = 3 3 cm.
Vì ∆ G E L đồng dạng ∆ G F S nên E L F S = G E G F
⇒ E L = G E . F S G F = 1 . 3 3 9 = 3 3
Vì (N) là khói nón cụt nên:
V N = 1 3 E L 2 + F S 2 + E L . F S E F = 728 π 9
Chọn đáp án D.

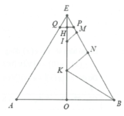
HD: Giả sử thiết diện là hình thang ABPQ
Gọi I, K lần lượt là tâm của đường tròn nhỏ và to.
Gọi M, N là hình chiếu của I, K lên một cạnh bên, điểm

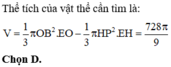

Đáp án C
Gọi r là bán kính đường tròn của hình trụ
Thể tích khối trụ là V = π r 2 h = 2 π ⇔ h = 2 r 2 với thể tích k = 2 π m 3
Chi phí để làm diện tích đáy hình trụ là T d = 6 S d = 6 π r 2 trăm nghìn đồng
Chi phí để làm diện tích nắp hình trụ là T n = 2 S n = 2 π r 2 trăm nghìn đồng
Chi phí để làm diện tích mặt bên hình trụ là T b = 4 S b = 8 π r h trăm nghìn đồng
Vậy tổng chi phí là:
T = 8 π r 2 + 8 π r h = 8 π r 2 + 2 r = 8 π r 2 + 1 r + 1 r
Áp dụng công thức Cosi, ta có:
r 2 + 1 r + 1 r ≥ 3 r 2 . 1 r . 1 r 3 = 3 ⇒ T ≥ 24 π ⇒ T min = 24 π
Dấu “=” xảy ra khi và chỉ khi:
r 2 = 1 r = k 2 π r ⇔ r = k 2 π 3