Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nếu trong \(5\) học sinh phải có ít nhất \(2\) học sinh nữ và \(2\) học sinh nam thì có \(2\) trường hợp :
\(2\) nam \(3\) nữ, có : \(C^2_{10}.C^3_{10}\) cách:
\(3\) nam và \(2\) nữ, có : \(C^3_{10}.C^2_{10}\) cách:
Vậy tất cả có : \(2.C^2_{10}.C^3_{10}=10800\) cách.
b) Nếu trong \(5\) học sinh phải có ít nhất \(1\) học sinh nữ và \(1\) học sinh nam thì có 4 trường hợp :
\(1\) nam và \(4\) nữ, có: \(C^1_{10}.C^4_{10}\) cách.
\(2\) nam và \(3\) , có : \(C^2_{10}.C^3_{10}\) cách.
Còn lại bn tự lm nha, mỏi tay quá

Đáp án B
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản
Lời giải:
Chọn 2 học sinh trong 20 học sinh có C 20 2 = 190 ⇒ n ( Ω ) = 190 .
Gọi X là biến cố 2 học sinh được chọn trong đó có cả nam và nữ
Chọn 1 học sinh nam trong 8 nam có 8 cách, chọn 1 học sinh nữ trong 12 nữ có 12 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n(X) = 8.12 = 96.
Vậy P = n ( X ) N ( Ω ) = 48 95 .

Đáp án : A
Để lựa chọn được hai ban thỏa mãn yêu cầu, ta chia làm hai công đoạn.
Công đoạn 1: Chọn một học sinh giỏi nữ, có 9 cách thực hiện.
Công đoạn 2. Chọn một học sinh giỏi nam, có 7 cách thực hiện.
Vậy theo quy tắc nhân, sẽ có 9.7=63 cách lựa chọn.

Đáp án C.
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản
Lời giải:
Chọn 3 học sinh trong 10 học sinh có C 10 3 cách => n ( Ω ) = C 10 3 = 120 .
Gọi X là biến cố trong 3 học sinh được chọn có ít nhất một học sinh nữ
Ta xét các trường hợp sau:
TH1. Chọn 1 học sinh nữ và 2 học sinh nam => có C 7 2 . C 3 1 = 63 cách.
TH2. Chọn 2 học sinh nữ và 1 học sinh nam => có C 7 1 . C 3 2 = 21 cách.
TH3. Chọn 3 học sinh nữ và 0 học sinh nam => có C 3 3 = 1 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n(X) = 63 + 21 + 1 = 85.
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = 85 120 = 17 24 .

a. Chọn bất kì 5 học sinh từ 50 học sinh có: \(C_{50}^5\) cách
b. Lớp có 20 học sinh nam. Chọn 5 bạn trong đó có 2 bạn nam (suy ra 3 bạn nữ) đồng nghĩa: chọn 2 nam từ 20 nam và 3 nữ từ 30 nữ
\(\Rightarrow\) Có \(C_{20}^2.C_{30}^3\) cách
c. Số cách chọn 5 bạn toàn là nữ: \(C_{30}^5\) cách
Số cách chọn 5 bạn có ít nhất 1 nam: \(C_{50}^5-C_{30}^5\) cách



Trường hợp 1: Chọn 3 nữ, 2 nam ⇒ có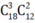 cách chọn
cách chọn
Trường hợp 2: Chọn 4 nữ, 1 nam có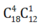 cách chọn
cách chọn
Do đó có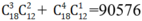 cách chọn.
cách chọn.
Chọn B.