

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D.
Phương pháp
Công thức tính diện tích xung quanh hình nón có bán kính đáy , R chiều cao h và đường sinh l: S x q = π R l .
Cách giải:
Công thức tính diện tích xung quanh hình nón có bán kính đáy , R chiều cao h và đường sinh l: S x q = π R l .

C
Ta có: z = − i 3 i + 4 = 3 − 4 i nên phần thực 3 và phần ảo -4

Đáp án A.
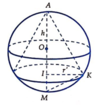
Kí hiệu như hình vẽ.
Ta thấy I K = r ' là bán kính đáy của hình chóp, A I = h là chiều cao của hình chóp.
Tam giác vuông tại K có IK là đường cao
⇒ I K 2 = A I . I M ⇒ r ' 2 = h . 2 r − h
Ta có V c o h p = 1 3 . π r ' 2 . h = 1 3 . π . h . h . 2 r − h = 4 3 π . h 2 . h 2 2 r − h .
Áp dụng bất đẳng thức Cauchy ta có
h 2 . h 2 . 2 r − h ≤ h 2 + h 2 + 2 r − h 3 27 = 8 r 3 27
⇔ V c h o p ≤ 4 3 π . 8 r 3 27 = 32 81 . π r 3
Dấu bằng xảy ra khi h 2 = 2 r − h ⇔ h = 4 r 3 . Vậy ta chọn A

Đáp án A
Diện tích toàn phần S t p ủa hình nón (N) là S t p = π R l + π R 2

Chọn B vì diện tích xung quanh của hình nón được tính bởi công thức S x q = 2 π r l