Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đối với tia tới SA, môi trường bán trụ có thể coi như có hai pháp tuyến vuông góc nhau.
Trong hai trường hợp ta luôn có: i = 45 ° , r = 30 °
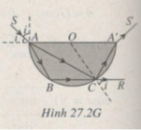
Do đó kết hợp các tính chất hình học, ta có hai đường đi của tia sáng như sau (Hình 27.2G):
+ SABCA’S’
+ SACR
(A, B, C, A’ chia nửa đường tròn thành ba phần bằng nhau).

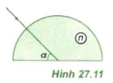
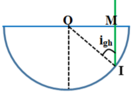
Vì tia sáng tới có đường kéo dài qua O nên tia tới SI vuông góc mặt phẳng trụ ⇒ góc i = 0 ⇒ tia sáng sẽ truyền thẳng vào khối trong suốt tới O.
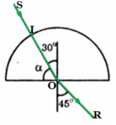
Tại O: tia sáng SO tạo với pháp tuyến ON của mặt phân cách phẳng một góc tới i.
Ta có: i = 90o - α
Mặt khác, góc giới hạn khi ánh sáng truyền từ khối bán trụ ra không khí được tính bởi công thức:
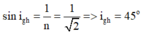
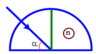
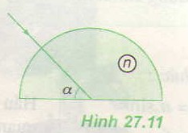
a) α = 60o
→ i = 90o – α = 30o → i < igh
Áp dụng định luật khúc xạ:
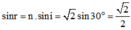
→ r = 45o. Vậy tia khúc xạ hợp với pháp tuyến của mặt phẳng phân cách của khối bán trụ góc khúc xạ 45o như hình vẽ.
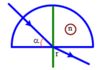
b) α = 45o
→ i = 90o – α = 45o → i = igh
→ r = 90o → Tia khúc xạ đi sát mặt phân cách của khối tròn như hình vẽ:
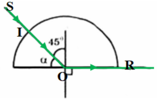
c) α = 30o
→ i = 90o – α = 60o → i > igh
→ Xảy ra phản xạ toàn phần, không có tia khúc xạ ra ngoài không khí. Đường đi của tia sáng được vẽ trên hình:

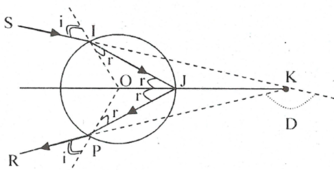
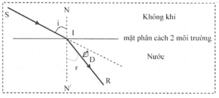
\(\left\{{}\begin{matrix}sin\left(i_{gh}\right)=\dfrac{1}{n}\xrightarrow[]{n=1,5}i_{gh}=41,81^o\\sin\left(i_1\right)=n.sin\left(r_1\right)\xrightarrow[i_1=17^o]{n=1,5}r_1=11,239^o\\r_1+r_2=A\xrightarrow[]{A=60^o}r_2=48,761^o>i_{gh}\\r_2+r_3=C\xrightarrow[]{C=60^o}11,239^o=r_1\end{matrix}\right.\)
\(n.sin\left(r_3\right)=sin\left(i_3\right)\Rightarrow i_3=17^o\)
Tia IJ quay theo chiều kim đồng hồ với góc SI một góc là:
\(D_1=17^o-11,239^o=5,761^o\)
Tia JK quay theo chiều kìm đồng hồ so với góc IJ một góc là:
\(D_2=180^o-2.48.761^o=82,478^o\)
Tia KR quay theo chiều kim đồng hồ so với góc JK là:
\(D_3=17^o-11,239^o=5,761^o\)
Vậy tia ló lệch tia tới:
\(D_1+D_2+D_3=94^o\)
⇒ Chọn A
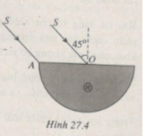

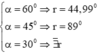


Tia SO có tia khúc xạ OJ truyền theo phương một bán kính (HÌnh 27.1G). Do đó tại J, góc tới bằng 0. Tia sáng truyền thẳng qua không khí.
Ta có D = i – r = 45 ° – 30 ° = 15 °