Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt giá phòng là x. Thu nhập f(x)
bài toán được phát biểu lại dưới dạng thuần túy Toán học như sau:
Tìm x sao cho f(x) lớn nhất biết rằng khi x = 400 thì f(400) = 400x50, mỗi khi x tăng thêm 20 đơn vị thì f(x+20k) = (x+20k)x(50-2k).
Giá đã tăng: x - 400 (ngàn đồng).
Số phòng cho thuê giảm nếu giá là x:

Số phòng cho thuê với giá x là:

Trả lời câu 1: Thay giá trị x = 500 vào biểu thức trên ta được giá trị cần tìm là 40.
Doanh thu là: f(x) =

Trả lời câu 2: Thế f(x) = 20200 vào phương trình trên, giải phương trình bậc hai, ta được x = 427,64 hoặc x= 472,36
f’(x)=

f’’(x)= -1/5
f’(x) = 0, tương đương x = 450.
và f’’(450) = -1/5< 0
Trả lời câu 3: Theo trên thì x = 450 là cực đại và là cực trị duy nhất.
Tuấn Anh Phan Nguyễn
Đặt giá phòng là x. Thu nhập f(x)
Bài toán được phát biểu lại dưới dạng thuần túy toán học như sau:
Tìm x sao cho f(x) lớn nhất biết rằng khi x = 400 thì f(400) = 400x50, mỗi khi x tăng thêm 20 đơn vị thì f(x+20k) = (x+20k)x(50-2k).
Giá đã tăng: x - 400 (ngàn đồng).
Số phòng cho thuê giảm nếu giá là x:

Số phòng cho thuê với giá x là:

Trả lời câu 1: Thay giá trị x = 500 vào biểu thức trên ta được giá trị cần tìm là 40.
Doanh thu là: f(x) =

Trả lời câu 2: Thế f(x) = 20200 vào phương trình trên, giải phương trình bậc hai, ta được x = 427,64 hoặc x= 472,36
f’(x)=

f’’(x)= -1/5
f’(x) = 0, tương đương x = 450.
và f’’(450) = -1/5< 0
Trả lời câu 3: Theo trên thì x = 450 là cực đại và là cực trị duy nhất.

Chọn D.
Chọn ngẫu nhiên 4 đại biểu có: C 20 4 cách chọn.Chọn ra 4 đại biểu có đủ 3 nước dẫn đến 3 trường hợp:
1) 2A – 1B – 1C, 1A – 2B – 1C, 1A – 1B – 2C dẫn đến có C 6 2 . 7 . 7 + 6 . C 7 2 . 7 + 6 . 7 . C 7 2 = 2499 cách.
2) Xét bài toán chọn 4 đại biểu đủ cả 3 nước mà toàn nam, dẫn đến các trường hợp:2A – 1B – 1C, 1A – 2B – 1C, 1A – 1B – 2C được C 4 2 . 5 . 5 + 4 . C 5 2 . 5 + 4 . 5 . C 5 2 = 550 cách.
3) Xét bài toán chọn 4 người đủ cả 3 nước toàn nữ: tương tự ta được 12 cách.
4) Vậy số trường hợp chọ được 4 đại biểu để mỗi nước đều có ít nhất một đại viểu và có cat đại biểu nam và đại biểu nữ là: 2499 – 550 – 12 = 1937
Vậy P= 1937 4845

Chọn B.
Phương pháp
Tính xác suất theo định nghĩa P A = n A n Ω với n(A) là số phần tử của biến cố A, n Ω là số phấn tử
của không gian mẫu.
Cách giải:
Số phần tử của không gian mẫu n Ω = C 20 2
Gọi A là biến cố “Hai người được chọn có it nhất một nữ” thì A là biến cố hai người được chọn không có nữ nào, tức là ta chọn 2 người trong số 7 nam.
Khi đó n A = C 7 2 ⇒ n A = C 10 2 - C 7 2
Xác suất để hai người được chọn có it nhất một nữ là P = C 10 2 - C 7 2 C 10 2 = 8 15






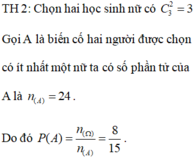
Chọn C