Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Tổng số viên bi trong hộp là 24. Gọi Ω là không gian mẫu.
· Lấy ngẫu nhiên 4 viên bị trong hộp em có: n Ω = C 24 4 = 10626 cách.
· Gọi A là biến cố lấy được các viên bi có đủ 3 màu. Em có các trường hợp sau
+) 2 bi đỏ, 1 bi vàng, 1 bi xanh có C 10 2 C 8 1 C 6 1 = 2160 cách
+) 1 bi đỏ, 2 bi vàng, 1 bi xanh có C 10 1 C 8 2 C 6 1 = 1680 cách
+) 1 bi đỏ, 1 bi vàng, 2 bi xanh có C 10 1 C 8 1 C 6 2 = 1200 cách
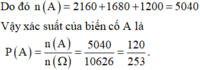

Chọn B
các trường hợp lấy được 4 viên bi trong đó số bi đỏ lớn hơn số bi vàng như sau:
Lấy 1 bi đỏ, 3 bi xanh có C 5 1 . C 4 3 cách; Lấy 2 bi đỏ, 2 bi xanh có C 5 2 . C 4 2 cách; Lấy 2 bi đỏ, 1 bi vàng, 1 bi xanh có C 5 2 . C 3 1 . C 4 1 cách; Lấy 3 bi đỏ, 1 bi xanh có C 5 3 . C 4 1 cách; Lấy 3 bi đỏ, 1 bi vàng có C 5 3 . C 3 1 cách; Lấy 4 bi đỏ: Có C 5 4 cách. Vậy số cách là: C 5 4 + C 5 1 . C 4 3 + C 5 2 . C 4 2 + C 5 3 . C 4 1 + C 5 2 . C 3 1 . C 4 1 + C 5 3 . C 3 1 = 275

Đáp án C
Để xác định biến cố, ta xét các trường hợp sau:
+) 2 bi xanh và 1 bi đỏ, suy ra có C 5 2 . C 4 1 = 40 cách.
+) 3 bi xanh và 0 bi đỏ, suy ra có C 5 3 = 10 cách.
Suy ra xác suất cần tính là P = 40 + 10 C 9 3 = 25 42

Giả sử trong tình huống xấu nhất ta chọn ngẫu nhiên 13 viên bi mà chỉ có bi màu vàng và màu xanh. Do để được chắc chắn 2 viên bi màu đỏ ta cần chọn thêm 2 viên bi nữa. Vậy cần chọn ít nhất 15 viên bi để chắc chắn được ít nhất 2 viên bi màu đỏ. Chọn B






Đáp án A
Lấy 8 viên chỉ có 2 màu :