Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
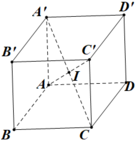
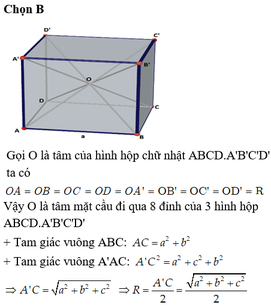
Gọi I là giao điểm các đường chéo của hình hộp thì I là tâm mặt cầu cần tìm.
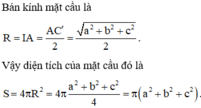

Chọn đáp án C
Bán kính r của mặt cầu ngoại tiếp hình hộp chữ nhật có ba kích thước a, b, c được tính theo công thức

Mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật có tâm là tâm của hình hộp chữ nhật đó và có bán kính bằng nửa độ dài đường chéo của hình hộp
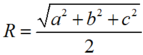
Diện tích của hình cầu đó là:
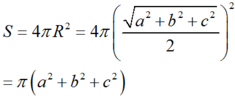
Chọn: C

Ta dễ thấy ba điểm A, B, C thuộc mặt phẳng ![]() , 3 mặt cầu là ở ngoài nhau. Mỗi mặt phẳng tiếp xúc với hai mặt cầu thì sẽ có hai tình huống.
, 3 mặt cầu là ở ngoài nhau. Mỗi mặt phẳng tiếp xúc với hai mặt cầu thì sẽ có hai tình huống.
1. Cả 3 mặt cầu ở cùng một nửa không gian chia bởi mặt phẳng tiếp xúc. Có 2 mặt phẳng như vậy.
2. Mặt phẳng tiếp xúc chia 2 mặt cầu về một phía và phía còn lại chứa mặt cầu kia. Có 4 mặt phẳng tiếp xúc chia mặt cầu lớn và mặt cầu nhỏ ở cùng một bên. Có một mặt phẳng tiếp xúc chia 2 mặt cầu nhỏ về một bên (ở đây do R + r + d ( A, BC ) nên mới tồn tại 1 mặt phẳng tiếp xúc theo yêu cầu, nếu R + r + d > d ( A, BC ) thì sẽ tồn tại 2 mặt phẳng tiếp xúc)
Đáp án cần chọn là B

Đáp án B.
![]()
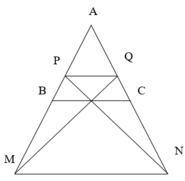
Do ![]() nên các khoảng cách từ A đến (P) gấp đôi khoảng cách từ B,C đến (P). gọi M, N lần lượt là điểm đối xứng của A qua B,C. và P,Q là điểm trên canh AB,AC sao cho AP=2BP, AQ=2QC. Bài toán quy về tìm các mp (P) chính là các mặt phẳng đi qua MN,MQ,NP,PQ sao cho d(A,(P))=2.
nên các khoảng cách từ A đến (P) gấp đôi khoảng cách từ B,C đến (P). gọi M, N lần lượt là điểm đối xứng của A qua B,C. và P,Q là điểm trên canh AB,AC sao cho AP=2BP, AQ=2QC. Bài toán quy về tìm các mp (P) chính là các mặt phẳng đi qua MN,MQ,NP,PQ sao cho d(A,(P))=2.
TH1: d(A, MQ)=2 nên chỉ có duy nhất 1 mp (P) qua PQ sao cho d(A,(P))=2.
TH2: d(A;MN), d(A;MQ), d(A,NP) đều lớn hơn 2 nên mỗi TH sẽ có 2 mp qua các cạnh MN,MQ,NP sao cho khoảng cách từ A đến nó bằng 2
Vậy có tất cả 7 mp thỏa mãn yêu cầu.

Đáp án B
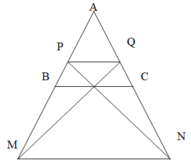
A B = A C = 13 , B C = 4 , d ( A , B C ) = 3 . Do R 1 = 2 R 2 = 2 R 3 nên các khoảng cách từ A đến (P) gấp đôi khoảng cách từ B,C đến (P). gọi M, N lần lượt là điểm đối xứng của A qua B,C. và P,Q là điểm trên canh AB,AC sao cho A P = 2 B P , A Q = 2 Q C . Bài toán quy về tìm các mp (P) chính là các mặt phẳng đi qua MN,MQ,NP,PQ sao cho d ( A , ( P ) ) = 2
TH1: d ( A , P Q ) = 2 nên chỉ có duy nhất 1 mp (P) qua PQ sao cho d ( A , ( P ) ) = 2
TH2: d ( A ; M N ) , d ( A , M Q ) , d ( A ; N P ) đều lớn hơn 2 nên mỗi TH sẽ có 2 mp qua các cạnh MN,MQ,NP sao cho khoảng cách từ A đến nó bằng 2
Vậy có tất cả 7 mp thỏa mãn yêu cầu

Đáp án A.
Bốn tâm của các bi nhỏ cùng với tâm của các bi lớn tạo thành hình chóp tứ giác đều có cạnh đáy bằng 2 và cạnh bên bằng 3. Khi đó chiều cao của hình chóp đều này là 7 .
Khoảng cách từ tâm của bi lớn đến đáy của hình hộp là 7 + 1 .
Do đó chiều cao của hình hộp là 2 . 7 + 1 = 2 + 2 7 .

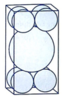
Đáp án A