Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi cạnh hình vuông là a (cm) thì diện tích hình vuông là a^2 (cm^2)
Chiều dài hình chữ nhật là a+4 (cm) , chiều rộng hình chữ nhật là a-3 (cm) thì diện tích hình chữ nhật là (a+4)(a-3) (cm^2)
ĐK : a >3
Vì diện tích hai hình bằng nhau nên ta có phương trình :
a^2= (a-3)(a+4)
<=> a^2= a^2+a-12
<=> a=12 (t/m đk)
Vậy chu vi hình chữ nhật là (12-3)(12+4)=144 (cm^2)
Gọi chiều dài vuông là x (x > 3) (cm)
=> Diện tích vuông là: x2 (cm2)
=> Chiều rộng hcn là: x - 3 (cm)
=> Chiều dài hcn là: x + 4 (cm)
=> Diện tích hcn là (x - 3)(x + 4)
Ta có phương trình sau:
x2 = (x - 3)(x + 4)
<=> x2 = x2 + x - 12
<=> x = 12 (cm)
=> Chiều dài hcn là 16 cm
=> Chiều rộng hcn là 9 cm
=> Chu vui hcn là (16 + 9) . 2 = 50 (cm)
Vậy...
Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
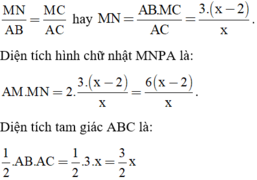
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
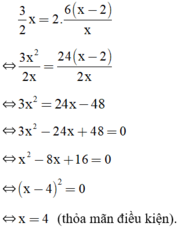
Vậy độ dài đoạn thẳng AC là 4cm.
đặt độ dài cạnh của hình vuông là x (cm) (x > 3)
=> ta có pt: (x + 2)(x - 3) = 50
<=> ... (tự trình bày ik)
<=> x = 8 (tmđk)
vậy độ dài cạnh của hv là 8cm
anh chỉ em chỗ tự trình bày á chứ em trình bày không ra được 8
Đáp án B
Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
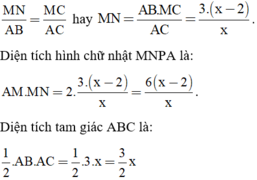
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
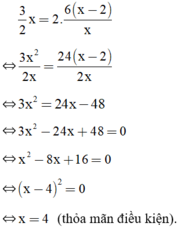
Vậy độ dài đoạn thẳng AC là 4cm.
độ dài cạnh còn lại của HCN :
132- 52=144
=> cạnh còn lại = 12 cm
S hcn :
12 . 5=60 cm
Diện tích hình chữ nhật hay diện tích hình vuông là:
18. 8 = 144 (m2)
Độ dài cạnh hình vuông đó là:
\(\sqrt{144}=12\) (m)
Gọi độ dài cạnh của hình vuông là \(a (a >0)\)
Theo đề bài : \(S_{hv}=S_{hcn} \Leftrightarrow a^2=8.18 \Rightarrow a=12 (TM)\)
Vậy độ dài cạnh của hình vuông là \(12m\).
DBDC, viết các cặp góc tương ứng bằng nhau của hai tam giác đã cho. 
có AB = 3cm, AC = 4,5cm, BC = 6cm. 
có DE= 12cm, EF=9cm, DF = 6cm. Chứng minh 
. 
AC). Tính AN? 
nhọn. Trên cạnh Ox, đặt các đoạn thẳng OA = 6cm, OB = 18cm. Trên cạnh Oy, đặt các đoạn thẳng OC = 9cm, OD = 12cm.Chứng minh hai tam giác OAD và OCB đồng dạng. 
có 
và 
có MN = 6cm; MP = 8cm; 
đồng dạng với 
