

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Theo giả thiết có
![]()
Gọi N là trung điểm cạnh SA.
Ta có 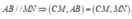
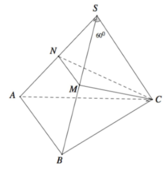
Có 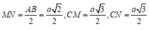
![]()
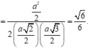
Chọn đáp án A.

Ta có C : y = 2 + 2 b - 1 , Gọi B b ; 2 + 2 b - 1 ; C c ; 2 + 2 b - 1 với b < 1 < c
Gọi H, K lần lượt là hình chiếu của B, C trên trục Ox
Ta có:
A B = A C ; B A C ^ = 90 o ⇒ C A K ^ + B A H ^ = 90 o = C A K ^ + A C K ^ ⇒ B A H ^ = A C K ^
Và
B H A ^ = C K A ^ = 90 o ⇒ ∆ A B H = ∆ C A K ⇒ A H = C K H B = A K
Hay 2 - b = 2 + 2 c - 1 2 + 2 b - 1 = c - 2 ⇔ b = - 1 c = 3
Vậy B ( -1;1 ), C ( 3;3 )
Đáp án A

Lấy F thuộc AC sao cho AD = AF. Khi đó tam giác ADF vuông cân ở A ==> DFAˆ=450→DFCˆ=1350
Ta có:
BDEˆ=1800−EDCˆ−ADCˆ=1800−900−ADCˆ=900−ADCˆ
ACDˆ=900−ADCˆ (vì tam giác ADC vuông ở A)
Suy ra ACDˆ=BDEˆ
Mặt khác:
BD = AB - AD
CF = AC - AF
AB = AC, AD = AF
Nên BD = CF.
Xét tam giác BDE và tam giác FCD:
BD = FC
BDEˆ=FCDˆ
EBDˆ=DFCˆ(=1350)
Suy ra ΔBDE = ΔFCD (g.c.g) ==> DE = DC
Mà tam giác EDC vuông ở D.
Suy ra tam giác EDC vuông cân ở D.