Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D
Gọi h1, h2 là độ cao của cột nước và cột thủy ngân.
Ta có H = h1 + h2 (1)
Khối lượng nước và thủy ngân bằng nhau:
⇒ S.h1.ρ1 = S.h2.ρ2 (2), trong đó S là diện tích đáy bình
Áp suất của nước và của thủy ngân lên đáy ống:
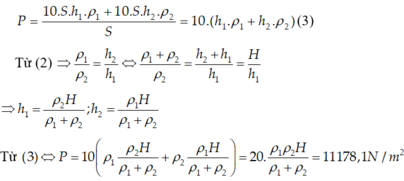

Đáp án: C
Do có hiện tượng mao dẫn nên thủy ngân trong ống thủy tinh bị tụt xuống một đoạn:
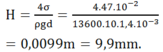
Áp suất thực của khí quyển tại vị trí đo là :
p = 760 + 9,9 = 769,9 mmHg.

Đápán: B
Khi trong ống không có nước:
![]()
Khi trong ống có nước:
![]()
Lực nén tại A trong hai trường hợp tỉ lệ với áp suất nên ta có:
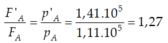

Do có hiện tượng mao dẫn nên thủy ngân trong ống thủy tinh bị tụt xuống một đoạn:
![]()
Áp suất thực của khí quyển tại vị trí đo là p = 760 + 9,8 = 769,8mmHg.

Đáp án: D
Áp suất khí quyển cân bằng với áp suất của cột thủy ngân, do đó ta phải xác định được chiều cao cột thủy ngân khi cơn bão đến gần.
Muốn vậy trước tiên ta tìm chiều cao của cột thủy ngân tiêu chuẩn theo công thức:
pa = ρ.g.h
→ h = pa/( ρ.g) = 1,013.105 / (13590.10) = 0,745 m
Chiều cao cột thủy ngân khi cơn bảo đến gần là:
h’ = h -∆h = 0,725 m.
→ áp suất khí quyển lúc này: p’ = ρ.g.h’ = 0,986.105 Pa.
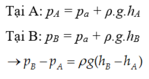

Gọi h1, h2 là độ cao của cột nước và cột thủy ngân.
Ta có H = h 1 + h 2 (1)
Khối lượng nước và thủy ngân bằng nhau S h 1 ρ 1 = S h 2 ρ 2 (2)
trong đó S là diện tích đáy bình
Áp suất của nước và của thủy ngân lên đáy ống:
P = 10 S h 1 ρ 1 + 10 S h 2 ρ 2 S = 10 ( h 1 ρ 1 + h 2 ρ 2 ) (3)
Từ (2) ⇒ ρ 1 ρ 2 = h 2 h 1 ⇔ ρ 1 + ρ 2 ρ 2 = h 2 + h 1 h 1 = H h 1 ⇒ h 1 = ρ 2 H ρ 1 + ρ 2 ; h 2 = ρ 1 H ρ 1 + ρ 2
( 3 ) ⇔ P = 10 ρ 1 ρ 2 H ρ 1 + ρ 2 + ρ 2 ρ 1 H ρ 1 + ρ 2 = 20 ρ 1 ρ 2 H ρ 1 + ρ 2 = 20. 1000.13600.0 , 6 1000 + 13600 = 11178 , 1 N / m 2
a