Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- hoa24092001yl
Đáp án:
Vòi thứ nhất chảy một mình mất 9h9h, vòi thứ hai mất 12h12h thì đầy bể.
Giải thích các bước giải:
Gọi thời gian vòi thứ nhất và vòi thứ hai chảy một mình để đầy bể lần lượt là x;y(h)(x;y>0)x;y(h)(x;y>0)
Khi đó, mỗi giờ, vòi thứ nhất chảy được 1x1x bế, vòi thứ hai chảy được 1y1y bể.
Theo giả thiết ta có hệ phương trình sau:
{3.1x+8.1y=15.1x+4.1y=89⇔{3.1x+8.1y=110.1x+8.1y=169⇒(10.1x+8.1y)−(3.1x+8.1y)=169−1⇔7.1x=79⇔1x=19⇒1y=112⇒{x=9(h)y=12(h){3.1x+8.1y=15.1x+4.1y=89⇔{3.1x+8.1y=110.1x+8.1y=169⇒(10.1x+8.1y)−(3.1x+8.1y)=169−1⇔7.1x=79⇔1x=19⇒1y=112⇒{x=9(h)y=12(h)
Vậy vòi thứ nhất chảy một mình mất 9h9h, vòi thứ hai mất 12h12h thì đầy bể.
Đáp án:
Vòi thứ nhất chảy một mình mất 9h9h, vòi thứ hai mất 12h12h thì đầy bể.
Giải thích các bước giải:
Gọi thời gian vòi thứ nhất và vòi thứ hai chảy một mình để đầy bể lần lượt là x;y(h)(x;y>0)x;y(h)(x;y>0)
Khi đó, mỗi giờ, vòi thứ nhất chảy được 1x1x bế, vòi thứ hai chảy được 1y1y bể.
Theo giả thiết ta có hệ phương trình sau:
{3.1x+8.1y=15.1x+4.1y=89⇔{3.1x+8.1y=110.1x+8.1y=169⇒(10.1x+8.1y)−(3.1x+8.1y)=169−1⇔7.1x=79⇔1x=19⇒1y=112⇒{x=9(h)y=12(h){3.1x+8.1y=15.1x+4.1y=89⇔{3.1x+8.1y=110.1x+8.1y=169⇒(10.1x+8.1y)−(3.1x+8.1y)=169−1⇔7.1x=79⇔1x=19⇒1y=112⇒{x=9(h)y=12(h)
Vậy vòi thứ nhất chảy một mình mất 9h9h, vòi thứ hai mất 12h12h thì đầy bể.

Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là x (giờ), (x > 2)
Trong một giờ:
- Vòi thứ nhất chảy được 1/x (bể)
- Vòi thứ hai chảy được 1/(x-2) (bể)
- Vì vòi thứ ba chảy ra trong 7,5 giờ thì cạn bể nên trong 1 giờ vòi thứ ba chảy được 2/15 (bể)
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước chảy ở bể ra nên ta có phương trình:

Vậy chỉ dùng vòi thứ nhất thì sau 10 giờ bể đầy nước
Đáp án: C

Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là x (giờ), (x > 0)
Trong một giờ:
- Vòi thứ nhất chảy được 1/x (bể)
- Vòi thứ hai chảy được 1/(x+4) (bể)
- Vòi thứ ba chảy được 1/6 (bể)
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước ở bể chảy ra nên ta có phương trình:
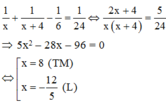
Vậy chỉ dùng vòi thứ nhất thì sau 8 giờ bể đầy nước
Đáp án: D

gọi 1/x là số nước chảy vào trong 1 h của vòi một
=> ... vòi hai là 1/X+6
ta có:
1/x+1/x+6 = 1/4
=> x bằng 6
. vậy nếu mở riêng từng vòi thì vòi 1 có thời gian là 6h
vòi hai là 10h

Đổi 2 giờ 55 phút = ![]() giờ
giờ
Gọi x (giờ) là thời gian chảy riêng đầy bể của vòi thứ nhất.
Điều kiện: x > 35/12
Khi đó thời gian chảy riêng đầy bể của vòi thứ hai là x + 2 (giờ)
trong 1 giờ, vòi thứ nhất chảy được 1/x (bể)
trong 1 giờ, vòi thứ hai chảy được 1/(x + 2 ) (bể)

Giá trị x = - 7/6 không thỏa mãn điều kiện bài toán.
Vậy vòi thứ nhất chảy riêng đầy bể trong 5 giờ
vòi thứ hai chảy riêng đầy bể trong 5 + 2 = 7 giờ

thời gian bể 1 chảy là x-1
thời gian bể một chảy trong 1 giờ là \(\frac{1}{x-1}\)
thời gian bể thứ 2 chảy là x
thời gian bể 2 chảy trong 1 giờ là \(\frac{1}{x}\)
4 giờ 48=\(\frac{24}{5}h\)
1 giờ 2 bể chảy \(1:\frac{24}{5}=\frac{5}{24}\left(h\right)\)
ta có pt:
\(\frac{1}{x}+\frac{1}{x-1}=\frac{5}{24}\)
\(24x-24+24x=5x\left(x+1\right)\)
\(48x+24=5x^2-5\)
\(5x^2-48x-29=0\)
\(\sqrt{\Delta}=2\sqrt{721}\)
\(x_1=\frac{48+2\sqrt{721}}{10}=\frac{24+\sqrt{721}}{5}\)
\(x_2=\frac{48-2\sqrt{721}}{10}\left(KTM\right)\)
vòi thứ 1 chảy số giờ là:
\(\frac{24+\sqrt{721}}{5}-1=\frac{19+\sqrt{721}}{5}\left(h\right)\)