K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
24 tháng 9 2021
Bài 2:
a. 3x(x - 6) - 2x2 = x2 + 6
<=> 3x2 - 18x - 2x2 - x2 - 6 = 0
<=> 3x2 - 2x2 - x2 - 18x - 6 = 0
<=> -18x - 6 = 0
<=> -18x = 6
<=> x = \(\dfrac{6}{-18}=\dfrac{-1}{3}\)
b. (x - 3)(x - 2) - 5 = x2 - 4x
<=> x2 - 2x - 3x + 6 - 5 - x2 + 4x = 0
<=> x2 - x2 - 2x - 3x + 4x + 6 - 5 = 0
<=> -x + 1 = 0
<=> -x = -1
<=> x = 1
c. (x + 5)2 - 8x = x2 + 15
<=> x2 + 10x + 25 - 8x - x2 - 15 = 0
<=> x2 - x2 + 10x - 8x + 25 - 15 = 0
<=> 2x + 10 = 0
<=> 2x = -10
<=> x = -5
d. x2 - 4x + 4 = 0
<=> x2 - 2.2.x + 22 = 0
<=> (x - 2)2 = 0
<=> x - 2 = 0
<=> x = 2
e. x2 + 8x + 16 = 0
<=> x2 + 2.x.4 + 42 = 0
<=> (x + 4)2 = 0
<=> x + 4 = 0
<=> x = -4
f. x2 - 36 = 0
<=> x2 - 62 = 0
<=> (x - 6)(x + 6) = 0
<=> \(\left[{}\begin{matrix}x-6-0\\x+6=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
g. (x + 3)2 - 16 = 0
<=> (x + 3)2 - 42 = 0
<=> (x + 3 + 4)(x + 3 - 4) = 0
<=> (x + 7)(x - 1) = 0
<=> \(\left[{}\begin{matrix}x+7=0\\x-1=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=-7\\x=1\end{matrix}\right.\)
24 tháng 9 2021
k: Ta có: \(\left(x-2\right)\left(x^2+2x+4\right)-2x^3+8\)
\(=x^3-8-2x^3+8\)
\(=-x^3\)
LT
1
3 tháng 6 2021
\(\dfrac{2\left(5x+2\right)}{9}-1=\dfrac{4\left(33+2x\right)}{5}-\dfrac{5\left(1-11x\right)}{9}\)
\(\dfrac{10\left(5x+2\right)}{45}-\dfrac{45}{45}=\dfrac{36\left(33+2x\right)}{45}-\dfrac{25\left(1-11x\right)}{45}\)
\(50x-20-45=1188+72x-25+275x\)
\(50x-25=347x+1163\)
\(50x-347x=25+1163\)
\(-297x=1188\)
\(x=4\\ \)
d)
\(\dfrac{2\left(x-4\right)}{3}+\dfrac{3x+13}{8}=\dfrac{2\left(2x-3\right)}{5}+12\)
\(\dfrac{80\left(x-4\right)}{120}+\dfrac{15\left(3x+13\right)}{120}=\dfrac{40\left(2x-3\right)}{120}+\dfrac{1440}{120}\)
\(80x-320+45x+195=80x-120+1440\)
\(125x-125=80x+1320\)
\(125x-80x=125+1320\)
\(45x=1445\)
\(x=\dfrac{1445}{45}\) \(=\dfrac{289}{9}\)
LT
3 tháng 6 2021
Sai rồi anh ơi 😢
c)S={-4}
d)S={49}
Sách nó viết thế chứ em ko biết nha
VD
29 tháng 5 2022
Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2023
1. Đ
2. Sai (câu này D mới đúng, C chỉ đúng khi thêm điều kiện a khác 0)
3. A
4. D
5. Sai, B đúng
6. Đ
7. Đ
8. S, đáp án đúng là A
9. S, đáp án đúng là C
10. Đ
11. Đ
12. Đ
13. S, đáp án đúng là A
14. Đ
15. Đ
16. A
17. A đúng (câu này bản thân đề bài ko rõ ràng, lẽ ra phải ghi là "phương trình bậc nhất một ẩn có thể có bao nhiêu nghiệm")
18. C mới là đáp án đúng
PM
1
6 tháng 5 2022
-Bài 3:
2) -Áp dụng BĐT Caushy Schwarz ta có:
\(A=\dfrac{1}{x^3+3xy^2}+\dfrac{1}{y^3+3x^2y}\ge\dfrac{\left(1+1\right)^2}{x^3+3xy^2+3x^2y+y^3}=\dfrac{4}{\left(x+y\right)^3}\ge\dfrac{4}{1^3}=4\)-Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
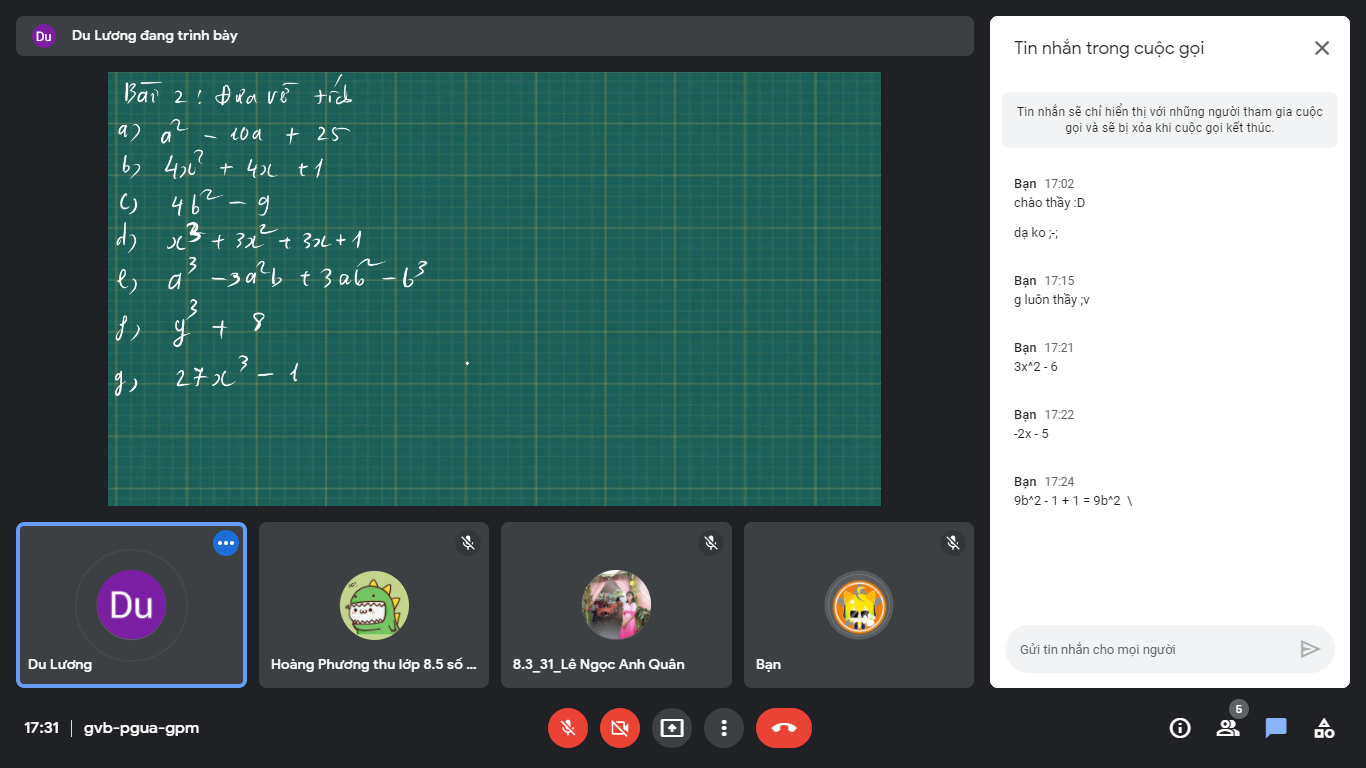
\(a,a^2-10a+25=\left(a-5\right)^2\\ b,4x^2+4x+1=\left(2x+1\right)^2\\ c,4x^2-9=\left(2x-3\right)\left(2x+3\right)\\ d,x^3+3x^2+3x+1=\left(x+1\right)^3\\ e,a^3-3a^2b+3ab^2-b^3=\left(a-b\right)^3\\ f,y^3+8=\left(y+2\right)\left(y^2-2y+4\right)\\ g,27x^3-1=\left(3x-1\right)\left(9x^2+3x+1\right)\)
\(a^2-10x+25=\left(a-5\right)^2\)
b/ \(4x^2+4x+1=\left(2x+1\right)^2\)
c/ \(4b^2-9=\left(2b-3\right)\left(2b+3\right)\)
d/ \(x^3+3x^2+3x+1=\left(x+1\right)^3\)
e/ \(a^3-3a^2b+3ab^2-b^3=\left(a-b\right)^3\)
f/ \(y^3+8=\left(y+2\right)\left(y^2-2y+4\right)\)
g/ \(27x^3-1=\left(3x-1\right)\left(9x^2+3x+1\right)\)