
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


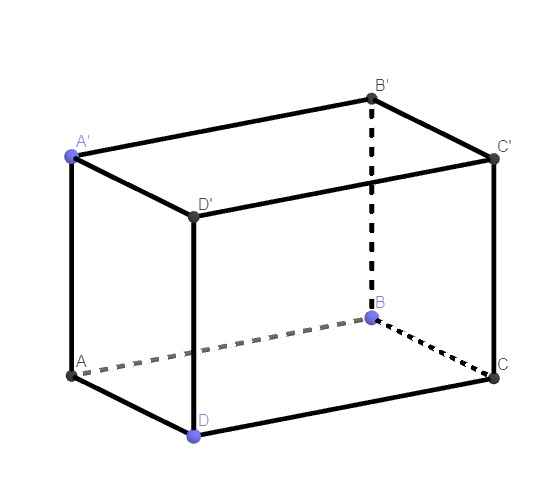
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)

Gọi số học sinh nam là a (18<a<36)
Số học sinh nam biết bơi là b, số học sinh nữ biết bơi là c (lẻ)
\(\Rightarrow\dfrac{C_b^1.C_c^1}{C_a^1.C_{36-a}^1}=\dfrac{140}{299}\)
\(\Rightarrow299bc=140a\left(36-a\right)\)
Do \(a+36-a=36\) chẵn \(\Rightarrow\) a và \(36-a\) cùng tính chẵn lẻ
Mặt khác 299 và 140 nguyên tố cùng nhau \(\Rightarrow a\left(36-a\right)⋮299\left(=13.23\right)\)
Do 18<a<36 \(\Rightarrow\) mỗi số a và 36-a không thể đồng thời chia hết 13 và 23
\(\Rightarrow\) a chia hết cho 13 hoặc 23
TH1: \(a⋮13\Rightarrow a=26\Rightarrow36-a=10\) không chia hết 23 (loại)
TH2: \(a⋮23\Rightarrow a=23\Rightarrow36-a=13\) (thỏa mãn)
\(\Rightarrow bc=140\left(=4.5.7\right)\)
Do c lẻ, và \(c< 36-a=13\), đồng thời \(b< a=23\)
TH1: \(c=5\Rightarrow b=28>a\left(ktm\right)\)
TH2: \(c=7\Rightarrow b=20\) (thỏa mãn)
Vậy có 20 học sinh nam biết bơi


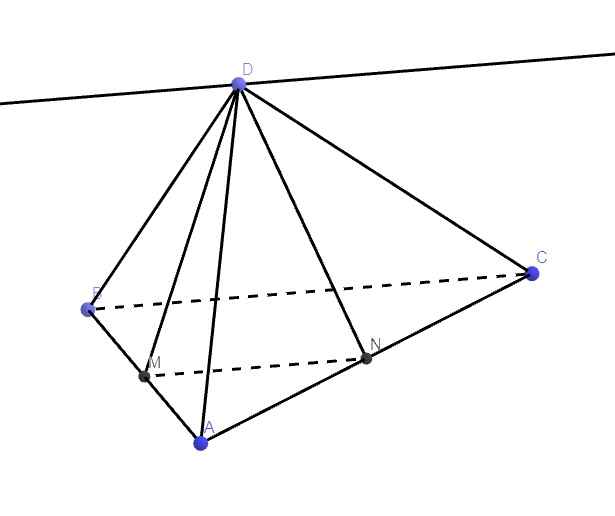
Giả thiết suy ra MN là đường trung bình tam giác ABC \(\Rightarrow MN||BC\)
Mà \(\left\{{}\begin{matrix}MN=\left(DMN\right)\cap\left(ABC\right)\\BC=\left(BCD\right)\cap\left(ABC\right)\end{matrix}\right.\)
Và D là 1 điểm chung của (BCD) và (DMN)
\(\Rightarrow\) Giao tuyến của (BCD) và (DMN) phải là 1 đường thẳng qua D và song song MN (hoặc BC)

Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF

Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)

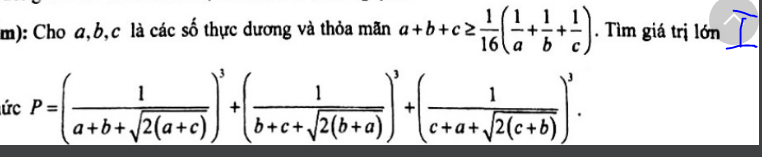 mọi người giúp em với em cảm ơn nhiều lắmmmmm
mọi người giúp em với em cảm ơn nhiều lắmmmmm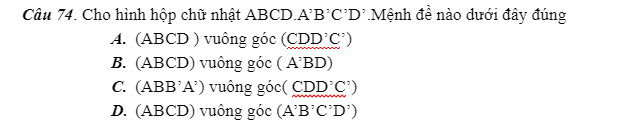
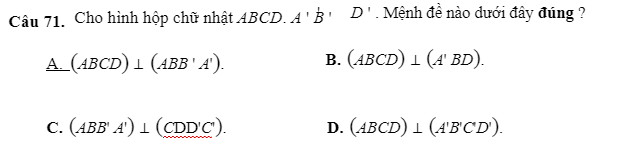
 mọi người giúp em với em cảm ơn nhiều lắm
mọi người giúp em với em cảm ơn nhiều lắm







\(\left(ab+bc+ca\right)^2\ge3abc\left(a+b+c\right)\Rightarrow\dfrac{ab+bc+ca}{abc}\ge\dfrac{3\left(a+b+c\right)}{ab+bc+ca}\)
\(\Rightarrow a+b+c\ge\dfrac{1}{16}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{1}{16}\left(\dfrac{ab+bc+ca}{abc}\right)\ge\dfrac{3}{16}\left(\dfrac{a+b+c}{ab+bc+ca}\right)\)
\(\Rightarrow ab+bc+ca\ge\dfrac{3}{16}\)
Ta có:
\(a+b+\sqrt{2\left(a+c\right)}=a+b+\sqrt{\dfrac{a+c}{2}}+\sqrt{\dfrac{a+c}{2}}\ge3\sqrt[3]{\dfrac{\left(a+b\right)\left(a+c\right)}{2}}\)
\(\Rightarrow\left(\dfrac{1}{a+b+\sqrt{2\left(a+c\right)}}\right)^3\le\dfrac{2}{27\left(a+b\right)\left(a+c\right)}\)
Tương tự và cộng lại:
\(P\le\dfrac{2}{27}\left(\dfrac{1}{\left(a+b\right)\left(a+c\right)}+\dfrac{1}{\left(a+b\right)\left(b+c\right)}+\dfrac{1}{\left(a+c\right)\left(b+c\right)}\right)\)
\(P\le\dfrac{4}{27}.\dfrac{a+b+c}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
Mặt khác:
\(\left(a+b\right)\left(b+c\right)\left(c+a\right)=\left(a+b+c\right)\left(ab+bc+ca\right)-abc\)
\(=\left(a+b+c\right)\left(ab+bc+ca\right)-\sqrt[3]{abc}.\sqrt[3]{ab.bc.ca}\)
\(\ge\left(a+b+c\right)\left(ab+bc+ca\right)-\dfrac{1}{3}.\left(a+b+c\right).\dfrac{1}{3}\left(ab+bc+ca\right)\)
\(=\dfrac{8}{9}\left(a+b+c\right)\left(ab+bc+ca\right)\)
\(\Rightarrow P\le\dfrac{4}{27}.\dfrac{a+b+c}{\dfrac{8}{9}\left(a+b+c\right)\left(ab+bc+ca\right)}=\dfrac{1}{6\left(ab+bc+ca\right)}\le\dfrac{1}{6.\dfrac{3}{16}}=\dfrac{8}{9}\)
cảm ơn thầy nhieefuuuuuuuuu ạ