K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
I3
23 tháng 11 2021
ƯC của(−15;+20) là: {±1;±5}
đây là theo hiểu biết của mk thôi nha, ko chép ai đâu^^
0
11 tháng 10 2021
Khi chia 2021 số bất kỳ cho 2020 ta sẽ có mỗi số có một số dư trong 2020 số dư: 0, 1, 2,…, 2020. Do đó theo nguyên lý Dirichlet phải tồn tại ít nhất hai số có cùng số dư. Hiệu của hai số đó sẽ chia hết cho 2020.
DD
Đoàn Đức Hà
Giáo viên
21 tháng 11 2021
Bài 5:
a) \(23⋮\left(x-2\right)\Leftrightarrow x-2\inƯ\left(23\right)=\left\{-23,-1,1,23\right\}\)
\(\Leftrightarrow x\in\left\{-21,1,3,25\right\}\).
b) \(2x+1\inƯ\left(-12\right)\)mà \(2x+1\)là số lẻ nên \(2x+1\in\left\{-3,-1,1,3\right\}\)
\(\Leftrightarrow x\in\left\{-2,-1,0,1\right\}\).
c) \(x-1=x+2-3⋮\left(x+2\right)\Leftrightarrow3⋮\left(x+2\right)\)
mà \(x\)là số nguyên nên \(x+2\inƯ\left(3\right)=\left\{-3,-1,1,3\right\}\Leftrightarrow x\in\left\{-5,-3,-1,1\right\}\).
DD
Đoàn Đức Hà
Giáo viên
21 tháng 11 2021
Bài 4:
a) \(-18⋮3,15⋮3\Rightarrow-18a+15b⋮3\).
b) Theo a) ta có \(-18a+15b⋮3\)mà \(-2015⋮̸3\)nên không tồn tại hai số nguyên \(a,b\)thỏa mãn ycbt.
S
29 tháng 11 2021
\(a.120=2^3.3.5\)
\(320=2^6.5\)
\(ƯC\left(120;320\right)=\left\{40;80;120;160;200;...\right\}\)
\(ƯCLN\left(120;320\right)=2^3.5=40\)
\(b.455=5.7.13\)
\(950=2.5^2.19\)
\(ƯC\left(455;950\right)=\left\{5;10;15;20;25;...\right\}\)
\(ƯCLN\left(455;950\right)=5\)
\(c.126=2.3^2.7\)
\(108=2^2.3^3\)
\(306=2.3^2.17\)
\(ƯC\left(126;108;306\right)=\left\{18;36;54;72;...\right\}\)
\(ƯCLN\left(126;108;306\right)=2.3^2=18\)
DD
Đoàn Đức Hà
Giáo viên
22 tháng 11 2021
Bài 4:
a) \(x+xy-3y=4\)
\(\Leftrightarrow x-3+y\left(x-3\right)=1\)
\(\Leftrightarrow\left(x+y\right)\left(x-3\right)=1\)
mà \(x.y\)là số nguyên nên ta có bảng giá trị:
| x+y | 1 | -1 |
| x-3 | 1 | -1 |
| x | 4 | 2 |
| y | -3 | -3 |
b) \(BCNN\left(6,7\right)=42\)nên \(BC\left(6,7\right)=B\left(42\right)\).
\(200< 6k< 2000\Rightarrow33< k< 334\)
suy ra có \(334-33-1=300\)giá trị của \(x\)là bội của \(6\)mà \(200< x< 2000\).
\(200< 7l< 2000\Rightarrow28< l< 286\)
suy ra có \(286-28-1=257\)giá trị của \(x\)là bội của \(7\)mà \(200< x< 2000\).
\(200< 42m< 2000\Leftrightarrow4< m< 48\)
suy ra có \(48-4-1=43\)giá trị của \(x\)là bội của \(42\)mà \(200< x< 2000\)
Số giá trị của \(x\)thỏa mãn ycbt là: \(300+257-43=514\)(số)
31 tháng 7 2021
428=22.107
422=2.211
115=5.23
180=22.32.5
160=25.5
190=2.5.9
250=2.53
350=2.52.7
324=22.34
364=22.7.13
270=2.33.5
290=2.5.29
120=23.3.5
150=2.3.52
160=25.5
31 tháng 7 2021
\(428=2^2\cdot107\)
\(422=2\cdot211\)
\(115=5\cdot23\)
\(180=2^2\cdot3^2\cdot5\)
\(160=2^5\cdot5\)
\(190=2\cdot5\cdot19\)
\(250=2\cdot5^3\)
\(350=2\cdot5^2\cdot7\)
\(324=2^2\cdot3^4\)
\(364=2^2\cdot7\cdot13\)
\(270=3^3\cdot2\cdot5\)
\(290=2\cdot5\cdot29\)
\(120=2^3\cdot3\cdot5\)
\(150=5^2\cdot2\cdot3\)
\(160=2^5\cdot5\)
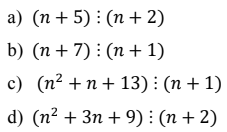
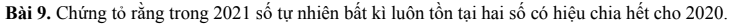
a) \(\Rightarrow\left(n+2\right)+3⋮\left(n+2\right)\)
\(\Rightarrow\left(n+2\right)\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Rightarrow n\in\left\{-5;-3;-1;1\right\}\)
b) \(\Rightarrow\left(n+1\right)+6⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(6\right)=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
\(\Rightarrow n\in\left\{-7;-4;-3;-2;0;1;2;5\right\}\)
c) \(\Rightarrow\left(n+1\right)^2-\left(n+1\right)+13⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(13\right)=\left\{-13;-1;1;13\right\}\)
\(\Rightarrow n\in\left\{-14;-2;0;12\right\}\)
d) \(\Rightarrow\left(n+2\right)^2-\left(n+2\right)+7⋮\left(n+2\right)\)
\(\Rightarrow\left(n+2\right)\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow n\in\left\{-9;-3;-1;5\right\}\)
Thanks bn iu nhìu!