K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DA
28 tháng 8 2021
\(\frac{1}{12}-\left(-\frac{1}{6}-\frac{1}{4}\right)\)
\(=\frac{1}{12}-\left(-\frac{2}{12}-\frac{3}{12}\right)\)
\(=\frac{1}{12}+\frac{2}{12}+\frac{3}{12}\)
\(=\frac{1}{2}\)
28 tháng 8 2021
Thanks bạn cute Jeon Koo Koo nhìu nha , tớ cảm ơn pạn rất nhìu :3
23 tháng 9 2019
(Nếu a và b song song hình ko cho song song nha e )
Ta có : \(\widehat{A_4}=\widehat{B_2}\)( 2 góc sole trong )
Mà \(\widehat{A_4}=\widehat{A_2}\)( 2 góc đối đỉnh ) ; \(\widehat{B_2}=\widehat{B_4}\)( 2 góc đối đỉnh )
=> \(\widehat{B_4}=\widehat{A_2}\)
TM
19 tháng 5 2017
Vì \(\left(3x-33\right)^{2016}\ge0;\left|y-7\right|\ge0\Leftrightarrow\left|y-7\right|^{2017}\ge0\)
=>\(\left(3x-33\right)^{2016}+\left|y-7\right|^{2017}\ge0\)
mà theo đề bài: \(\left(3x-33\right)^{2016}+\left|y-7\right|^{2017}\le0\)
=>\(\left(3x-33\right)^{2016}+\left|y-7\right|^{2017}=0\) <=>\(\left(3x-33\right)^{2016}=0;\left|y-7\right|^{2017}=0\)
- (3x-33)2016=0 <=> 3x-33=0 <=> 3x=33 <=> x=11
- |y-7|2017=0 <=> |y-7|=0 <=> y-7=0 <=> y=7
Vậy x=11 và y=7
30 tháng 1 2022
a: Xét ΔABM và ΔDBM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔABM=ΔDBM
b: Ta có: ΔABM=ΔDBM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
c: Ta có: BA=BD
nên ΔBAD cân tại B
mà BM là đường phân giác
nên BM là đường cao
d: Ta có: ΔABM=ΔDBM
nên MA=MD
Ta có: BA=BD
nên B nằm trên đường trung trực của AD(1)
Ta có: MA=MD
nên M nằm trên đường trung trực của AD(2)
Từ (1) và (2) suy ra BM là đường trung trực của AD
hay BM⊥AD
TN
1
10 tháng 1 2022
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
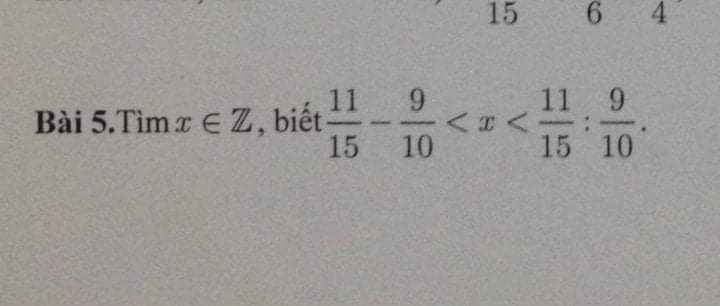
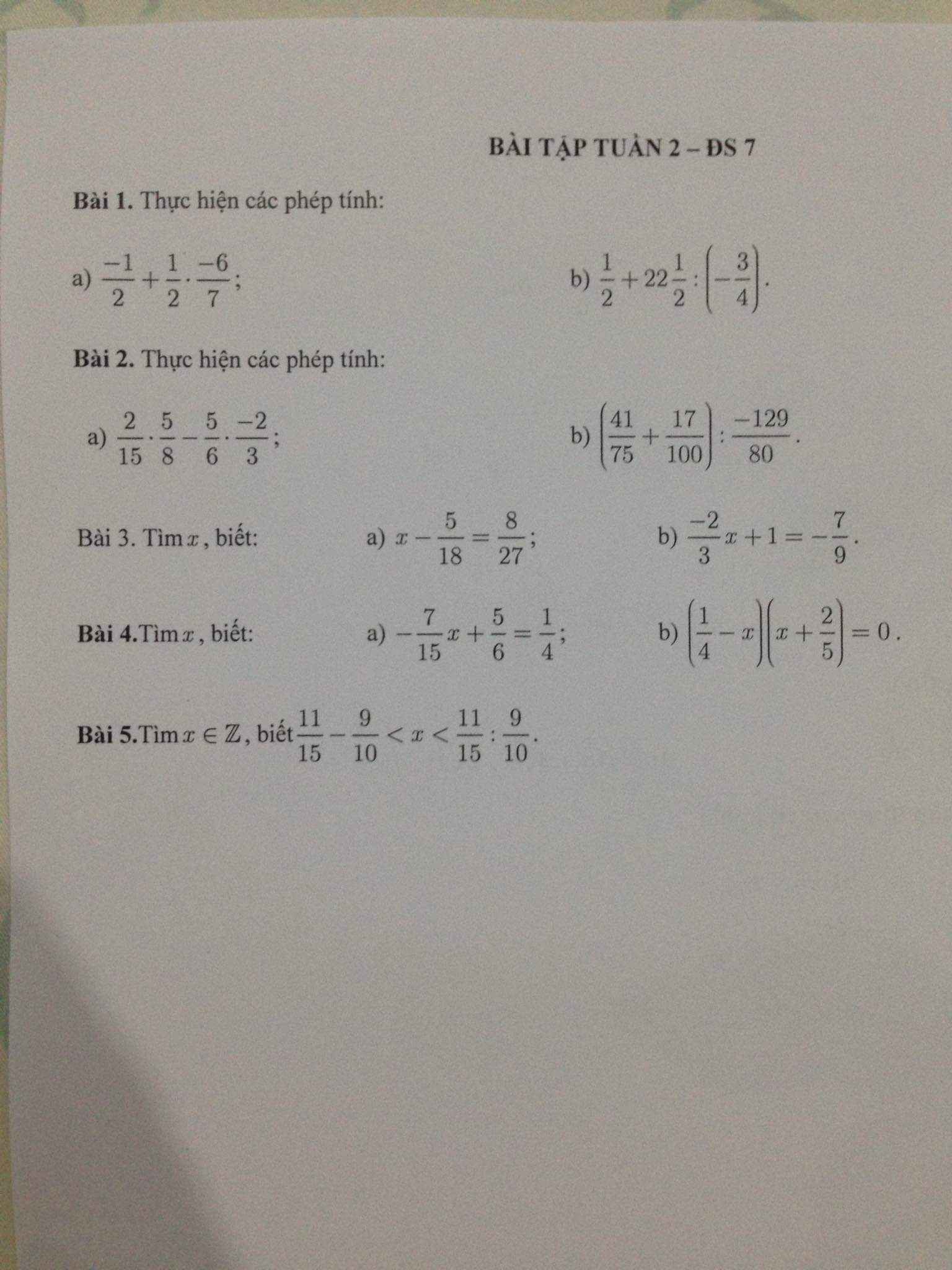
\(\dfrac{11}{15}-\dfrac{9}{10}< x< \dfrac{11}{5}:\dfrac{9}{10}\)
\(\Leftrightarrow\dfrac{22-27}{30}< x< \dfrac{11}{5}\cdot\dfrac{10}{9}\)
\(\Leftrightarrow\dfrac{-1}{6}< x< \dfrac{22}{9}\)
\(\Leftrightarrow x\in\left\{0;1;2\right\}\)