K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
Nguyễn Minh Quang
Giáo viên
9 tháng 9 2021
Bài 1
ta có a+3+b-3 =a +b chia hết cho 4
nên (b-a )(a+b) cũng chia hết cho 4
bài 2.
ta có: \(M=6x^2-5x-6-12xy+6y^2+6y-3x+2y+2027\)
\(=6\left(x-y\right)^2-8\left(x-y\right)+2021=24-16+2021=2029\)
NB
3
DD
Đoàn Đức Hà
Giáo viên
21 tháng 8 2021
Bài 2.
\(n^4-2n^3-n^2+2n=n\left(n^3-2n^2-n+2\right)=n\left[n^2\left(n-2\right)-\left(n-2\right)\right]\)
\(=n\left(n-2\right)\left(n^2-1\right)=\left(n-2\right)\left(n-1\right)n\left(n+1\right)\)
là tích của \(4\)số nguyên liên tiếp nên trong đó có ít nhất \(1\)thừa số chia hết cho \(4\), \(1\)thừa số chia hết cho \(3\), \(1\)thừa số chia hết cho \(2\)nhưng không chia hết cho \(4\)
do đó \(A\)chia hết cho \(2.3.4=24\).
Ta có đpcm.
DD
Đoàn Đức Hà
Giáo viên
21 tháng 8 2021
Bài 1:
\(2-x=2\left(x-2\right)^3\)
\(\Leftrightarrow\left(x-2\right)\left[2\left(x-2\right)^2-1\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\2\left(x-2\right)^2=1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=\pm\sqrt{\frac{1}{2}}+2\end{cases}}\)
NT
3
XO
30 tháng 7 2021
Ta có (a + b + c)3 = [(a + b) + c]3 = (a + b)3 + 3(a + b)2c + 3(a + b)c2 + c3
= a3 + b3 + 3ab(a + b) + 3(a + b)2c + 3(a + b)c2 + c3
= a3 + b3 + c3 + 3(a + b)[ab + (a + b)c + c2]
= a3 + b3 + c3 + 3(a + b)(ab + ac + bc + c2)
= a3 + b3 + c3 + 3(a + b)(b + c)(a + c)
\(\Rightarrow\left(a+b+c\right)^3=a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)(vì a + b + c = a3 + b3 + c3 = 1)
\(\Rightarrow\)a = -b hoặc b = -c hoặc c = -a
Khi a = -b thì c = 1
\(\Rightarrow\) A = 1
Tương tự khi b = -c thì a = 1
\(\Rightarrow\) A = 1
khi a = -c thì b = 1
\(\Rightarrow A=1\)
Vậy A = 1 trong cả 3 trường hợp trên
help pls
B
19 tháng 1 2022
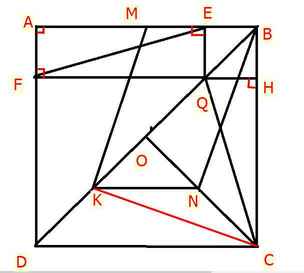
a) Ta có : \(\widehat{AEQ}=\widehat{EAF}=\widehat{AFQ}=90\)
➜ AEQF là hình chữ nhật ( DHNB hình chữ nhật )
b) Vì ABCD là hình vuông ➝ \(\widehat{ABD}=45\) ↔ \(\widehat{EBQ}=45\)
Mà ΔEBQ vuông tại E
➜ ΔEBQ vuông cân tại E
➝ EB = EQ
Mà \(\left\{{}\begin{matrix}FQ=AE\\AE+EB=AB\end{matrix}\right.\)
➞ QE + QF = AB
d) Ta có : AB = DC ( ABCD là hình vuông )
⇔ \(\dfrac{1}{2}DC=\dfrac{1}{2}AB=BM\)
Xét tam giác DOC có : K, N là trung điểm OD , OC
=> KN = \(\dfrac{1}{2}DC\) , KN // DC
Mà \(\dfrac{1}{2}DC=\dfrac{1}{2}AB=BM\) , DC // BM
=> KN = BM , KN // BM
=> KNBM là hình bình hành ( BDNB hình bình hành )
e) Ta có : KN ⊥ BC ( KN // AB // FH , FH ⊥ BC )
Lại có : AC ⊥ BD ( ABCD là hình vuông )
↔ CN ⊥ BD
Xét tam giác BCK có : CN ⊥ BD ; KN ⊥ BC
→ N là trực tâm Δ BCK
→ BN ⊥ KC
Mà BN // MK ( MBNK là hình bình hành )
→ MK ⊥ KC
➢ ĐPCM
\(\left(x-y\right)\left(x+y-3\right)\)
b, x^2-y^2-3x+3y
=(x^2-y^2)-(3x-3y)
= (x-y)(x+y)-3(x-y)
=(x-y)(x+y-3) dễ mè:>
c, bí ( đề sai zồi )