Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Một bạn học sinh làm 2 môn sẽ có 36 cách chọn đề, do đó 
Hai bạn Hùng và Vương có chung một mã đề thi thì cùng mã toán hoặc cùng mã tiếng anh do đó 
Vậy xác suất cần tính là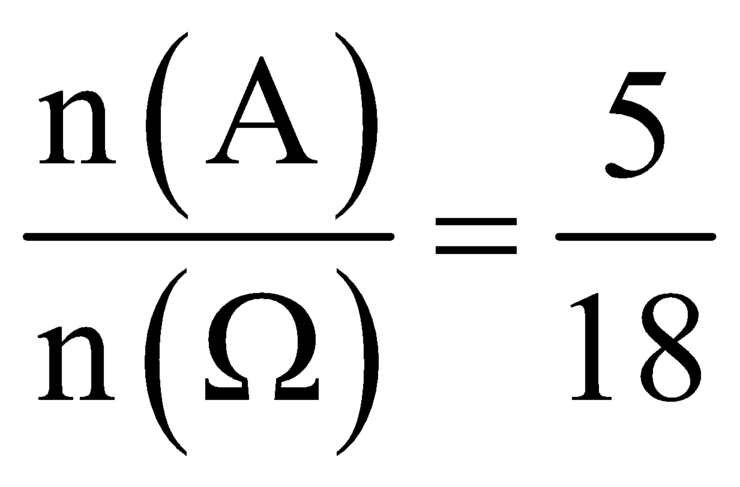 
Đáp án D
Không gian mẫu là: Ω = 6 4
TH1: Môn Toán trùng mã đề thi môn Tiếng Anh không trùng có:
Bạn Hùng chọn 1 mã toán có 6 cách và 6 cách chọn mã môn Tiếng Anh khi đó Vương có 1 cách là phải giống Hùng mã Toán và 5 cách chọn mã Tiếng Anh có 6.1.6.5 = 180 cách.
TH2: Môn Tiếng Anh trùng mã đề thi môn Toán không trùng có: 6.1.6.5 = 180 cách.
Vậy P = 180 + 180 6 4 = 5 18
Đáp án A.
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản trong bài toán sắp xếp đồ vật
Lời giải: Xếp 5 quyển Toán (coi Toán T1 và Toán T2 là một) có 5!.2! = 240 cách.
Khi đó, sẽ tạo ra 4 khoảng trống kí hiệu như sau: _T_T_T_T_T_
Xếp 3 quyển sách Tiếng Anh vào 4 khoảng trống giữa hai quyển toán có A 4 3 cách.
Xếp 1 quyển sách Văn vào 3 vị trí còn lại có 3 cách.
Vậy xác suất cần tính là P = 240 . A 4 3 . 3 10 ! = 1 210 .
Đáp án C
Để tạo một biển số xe ta thực hiện các bước sau:
+ Chọn hai chữ cái cho phần đầu có 
(mỗi chữ có 26 cách chọn)
+ Chọn 5 chữ số cho phần đuôi có 
(mỗi chữ số có 10 cách chọn)
Vậy có thể tạo ra được 
biển số xe
Trường hợp 1 : Trường đại học chỉ xét 1 trong 2 môn Toán hoặc Văn :
Có : \(2.C_6^2=30\) cách
Trường hớp 2 : Trường đại học xét cả 2 môn Toán và Văn :
Có : \(1.C_6^2=6\) cách
Vậy có các trường hợp là : 30+6=36 cách
trả lời rồi còn.....
hỏi gì nữa