
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(\sqrt{8^2+6^2}-\sqrt{16}+\dfrac{1}{2}\sqrt{\dfrac{4}{25}}\)
\(=10-4+\dfrac{1}{2}\cdot\dfrac{2}{5}=6+\dfrac{1}{5}=\dfrac{31}{5}\)

1) \(\left(\dfrac{-13}{17}-\dfrac{31}{52}\right)-\left(\dfrac{73}{52}-\dfrac{13}{17}+\dfrac{5}{6}\right)-\dfrac{3}{4}\)
\(=\dfrac{-13}{17}-\dfrac{31}{52}-\dfrac{73}{52}+\dfrac{13}{17}-\dfrac{5}{6}-\dfrac{3}{4}\)
\(=\left(\dfrac{-13}{17}+\dfrac{13}{17}\right)-\left(\dfrac{31}{52}+\dfrac{73}{52}\right)-\left(\dfrac{5}{6}+\dfrac{3}{4}\right)\)
\(=0-2-\dfrac{19}{12}\)
\(=-2-\dfrac{19}{12}\)
\(=\dfrac{-43}{12}\)



a: Xét ΔAHE vuông tại E và ΔAHI vuông tại I có
AH chung
góc EAH=góc IAH
=>ΔAHE=ΔAHI
b: HE=HI
=>HN=HM
Xét ΔAHN và ΔAHM có
AH chung
góc NHA=góc MHA
HN=HM
=>ΔAHN=ΔAHM
=>AN=AM
=>AH là trung trực của MN
=>AH vuông góc MN

a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: \(\widehat{HAD}+\widehat{BDA}=90^0\)
\(\widehat{CAD}+\widehat{BAD}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{HAD}=\widehat{CAD}\)
hay AD là tia phân giác của góc HAC
c: Xét ΔADH vuông tại H và ΔADK vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)
Do đó:ΔADH=ΔADK
Suy ra: AH=AK

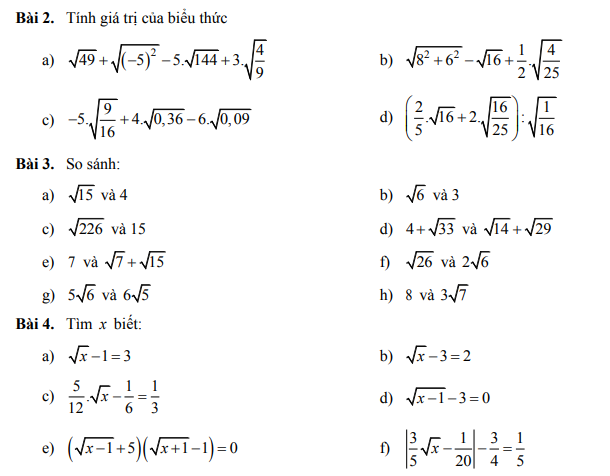 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
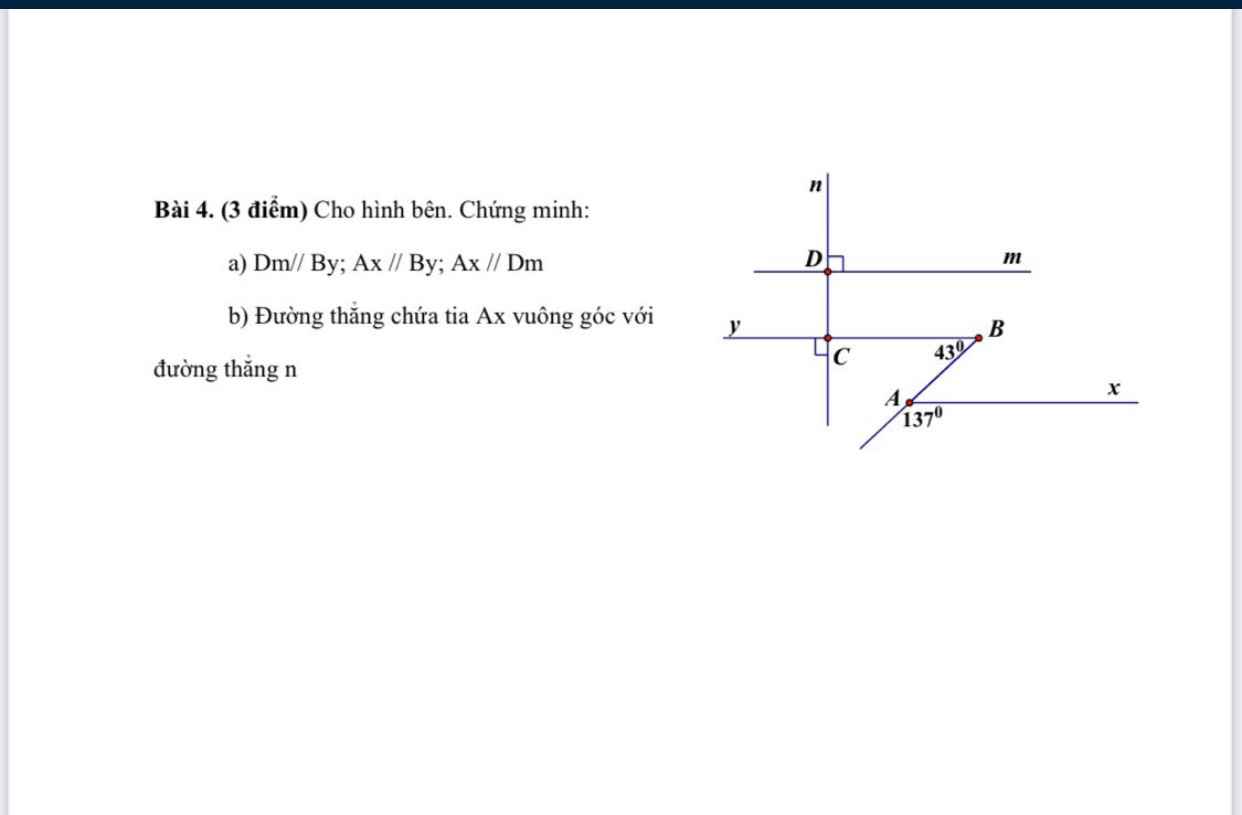
 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
