Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là:
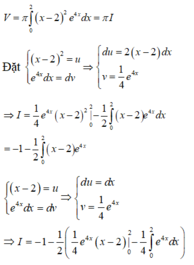
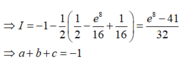
Đáp án C

1.
\(V=\pi\int\limits^1_0x^6dx=\dfrac{\pi x^7}{7}|^1_0=\dfrac{\pi}{7}\)
2.
\(F\left(x\right)=\int sin2xdx=-\dfrac{1}{2}cos2x+C\)
\(f\left(\dfrac{\pi}{4}\right)=1\Leftrightarrow-\dfrac{1}{2}cos\dfrac{\pi}{2}+C=1\Rightarrow C=1\)
\(\Rightarrow F\left(x\right)=-\dfrac{1}{2}cos2x+1\Rightarrow F\left(\dfrac{\pi}{6}\right)=\dfrac{3}{4}\)

Đáp án: D.
Hướng dẫn: Thể tích khối tròn xoay này được tính bởi
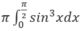

Chọn đáp án D.
Hoành độ giao điểm hai đồ thị là nghiệm của phương trình:
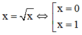
Thể tích cần tính:
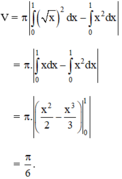
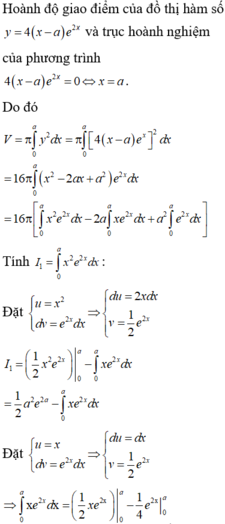
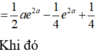
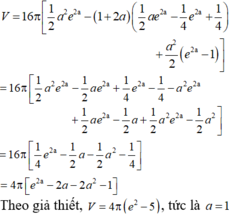
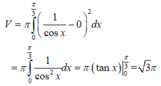
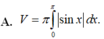
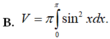
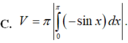
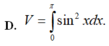
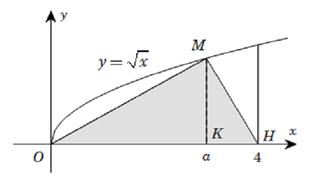

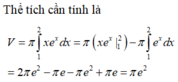
Tìm hoành độ giao điểm của hai dồ thị, ta có:
( x - 1 ) e 2 x = 0 => x = 1
Vậy thể tích của khối tròn xoay thu được khi quay (H) quanh Ox được tính bởi
Đặt: u = ( x - 1 ) 2 , d v e 4 x d x . Ta có du = 2(x -1)dx và v = e 4 x 4 .
Áp dụng công thức tích phân từng phần ta được
Đặt u 1 = x - 1 , d v 1 = e 4 x d x , ta có d u 1 = d x , v 1 = e 4 x 4
Vậy chọn đáp án A.