Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: △ ADC = △ BCD (c.c.c)
Suy ra : ∠ (ACD) = ∠ ( BDC)
Hay ∠ (OCD) = ∠ ( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Ta có: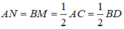 
Mà OA = OB ⇒ OM = ON
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: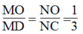 
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: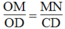 
Hệ quả định lí Ta-lét)
Suy ra: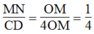 
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được:
(Hệ quả định lí Ta-lét)
Suy ra: 
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)
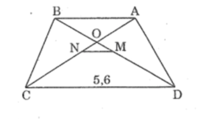
Xin lỗi Tú nhé hình mình vẽ chưa được cân lắm :( thông cảm
ABCD là hình thang cân nên AC = BD ; OA = OB ; OC = OD ; MN // AB // CD
\(MD=3.MO\Rightarrow OB=2.MO\) và \(OD=4.MO\)
Ta có : \(\frac{MN}{CD}=\frac{OM}{OD}=\frac{1}{4}\)\(\Rightarrow\)\(MN=\frac{1}{4}.CD=\frac{1}{4}.5,6=1,4\left(cm\right)\)
Mà \(\frac{AB}{CD}=\frac{OB}{OD}\Rightarrow\frac{AB}{CD}=\frac{1}{2}\)
\(\Rightarrow\)\(AB=\frac{1}{2}.CD=\frac{1}{2}.5,6=2,8\left(cm\right)\)
b) \(\frac{CD-AB}{2}=\frac{5,6-2,8}{2}=1,4\left(cm\right)\)
\(\Rightarrow\) \(MN=\frac{CD-AB}{2}\)
xong rùi nhé có gì sai sót bỏ qua dùm cái
Lời giải
a)
Ta có \(\left\{{}\begin{matrix}MD=MB\\NA=NC\end{matrix}\right.\) \(\Rightarrow\)MN//DC
\(\Rightarrow\Delta OMN\approx\Delta ODC\approx OBA\)
Tỷ số đồng dạng
\(\dfrac{OM}{OD}=\dfrac{MN}{DC}=\dfrac{ON}{OC}\)\(\Rightarrow MN=\dfrac{OM}{OD}.DC=\dfrac{1}{4}.5,6=1,4\left(cm\right)\)
\(\dfrac{OM}{OB}=\dfrac{MN}{AB}\Rightarrow AB=\dfrac{OB}{OM}.MN=2MN=2,8\left(cm\right)\)
b)
\(\left\{{}\begin{matrix}CD=4MN\\AB=2MN\end{matrix}\right.\)
\(\Rightarrow\dfrac{CD-AB}{2}=\dfrac{4MN-2MN}{2}=MN\)
a)Ta có :\(\left\{{}\begin{matrix}MD=MB\\NA=NC\end{matrix}\right.\)
\(\Rightarrow\text{MN//DC }\)
\(\Rightarrow\text{ΔOMN≈ΔODC≈OBA}\)
\(\Rightarrow\frac{OM}{OD}=\frac{MN}{DC}=\frac{ON}{OC}\)(Tỷ số đồng dạng)
\(\Rightarrow MN=\frac{OM}{OD}.DC=\frac{1}{4}.5,6=1,4cm\)
\(\frac{OM}{OB}=\frac{MN}{AB}\Rightarrow AB=\frac{OM}{OB}.MN=2MN=2,8cm\)
b)\(\left\{{}\begin{matrix}CD=4MN\\AB=2MN\end{matrix}\right.\)
\(\Rightarrow\frac{CD-AB}{2}=\frac{4MN-2MN}{2}=MN\)
Theo đề \(\frac{MD}{MO}=3\Leftrightarrow\frac{MD}{MO}+1=4\Leftrightarrow\frac{OD}{MO}=4\)
Cho P,Q là tđ AD,BC, Lại có M,N là tđ BD,AC nên có PM//AB, QN//AB
Lại có P,Q//AB//CD. Theo Ơ clit có M,N thuộc P,Q suy ra MN//CD.Theo Thales có
\(\frac{OD}{MO}=\frac{CD}{MN}=4\Rightarrow MN=\frac{CD}{4}=\frac{5,6}{4}=1,4\)
Vì BM=MD nên ta cũng có \(\frac{BM}{MO}=3\Leftrightarrow\frac{BM}{MO}-1=2\Leftrightarrow\frac{BO}{MO}=2\)
MN//AB nên \(\frac{BO}{MÔ}=\frac{AB}{MN}=2\Rightarrow AB=MN.2=...???\)
Ta có: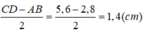
Vậy