Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do đó, \(SD=\dfrac{a^2}{2}:a\sqrt{2}=\dfrac{a\sqrt{2}}{4}\)
và \(AD=SA-SD=\dfrac{3a\sqrt{2}}{4}\)

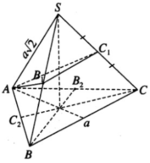
Giả sử mặt cầu đi qua đỉnh A của hình chóp và tiếp xúc với cạnh SB tại B1, tiếp xúc với cạnh SC tại C 1 . Khi đó mặt cầu cắt cạnh AB, AC lần lượt tại các điểm C 2 , B 2 . Mặt phẳng (SAB) cắt mặt cầu đó theo giao tuyến là một đường tròn. Đường tròn này tiếp xúc với SB tại B1 và đi qua A và C 2
Do đó, ta có: BB 1 2 = BA . BC 2
trong đó 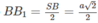
Do đó 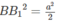
Vậy
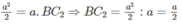
Điều đó chứng tỏ mặt cầu nói trên đi qua trung điểm C 2 của đoạn AB. Lí luận tương tự ta chứng minh được mặt cầu đó đi qua trung điểm B 2 của AC.

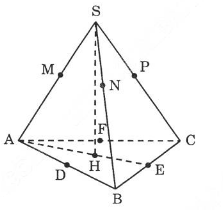
Gọi M, N, P theo thứ tự là các tiếp điểm của mặt cầu với các cạnh SA, SB, SC; D, E, F theo thứ tự là trung điểm của các cạnh AB, BC, CA, các điểm D, E, F đồng thời cũng là tiếp điểm của mặt cầu với các cạnh AB, BC, CA.
Ta có: AD = AF
BD = BE BC = AB
AB = BC = CA
\(\Delta ABC\) là tam giác đều (1)
Ta lại có AM = AD; BN = BD = AD
và SM = SN = SP
SM + AM = SN + NB
SA = SB
Chứng minh tương tự ta có: SA = SB = SC.
Gọi H là chân đường cao của hình chóp kẻ từ đỉnh S, ta có:
\(\Delta SHA=\Delta SHB=\Delta SHC\) => HA = HB = HC
H là tâm của tam giác đều ABC (2)
Từ (1) và (2) suy ra hình chóp S.ABC là hình chóp tam giác đều.

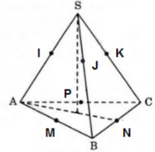
Gọi mặt cầu đã cho có tâm O và bán kính R.
Gọi M, N, P lần lượt là trung điểm của AB, BC và CA.
Gọi I,J và K lần lượt là tiếp điểm của các cạnh bên SA, SB, SC với mặt cầu:
+ Từ giả thiết ta suy ra: OI ⊥ SA; OM ⊥ AB
Xét tam giác OIA và tam giác OMA có:
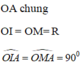
⇒ ∆ OIA = ∆OMA ( ch- cgv)
⇒ AM = AI.
Chứng minh tương tự có: BM= BJ và SI = SJ (1)
Mà AM = BM nên AI= BJ ; (2)
Từ (1) và (2) suy ra: SI+IA = SJ + BJ hay SA = SB (3)
* Chứng minh tương tự, ta có SB= SC (4).
Từ (3) và (4) suy ra: SA = SB = SC (*)
Mặt khác ; BM = BN (= BJ) và CN = CP (= CK)
Suy ra; AB = 2BM = BC = 2 CN = 2CP = CA
Do đó, tam giác ABC là tam giác đều (**)
Từ (*) và (**) suy ra, S. ABC là hình chóp tam giác đều.

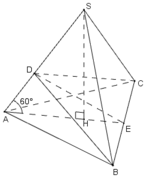
a)
+ Gọi H là hình chiếu của S trên (ABC)
⇒ AH là hình chiếu của SA trên (ABC)
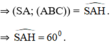
Gọi E là trung điểm BC
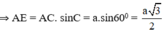
H là tâm của Δ đều ABC.


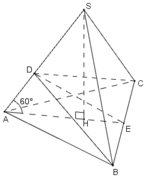
S H = S A 2 - A H 2 = a
Thể tích khối chóp S.ABC là:
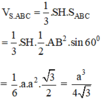
⇒ Thể tích khối chóp S.DBC là:
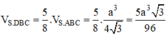


Gọi giao điểm thứ hai của mặt cầu với đường thẳng SA là D, ta có:
Do đó