Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng với ΔBHA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: BA^2=BH*BC
=>BM^2=BH*BC
=>BM/BH=BC/BM
=>ΔBMC đồng dạng với ΔBHM
=>góc BMH=góc BCM

Bài 3:
a: \(A=\dfrac{3\left(x+4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{3}{x-4}\)
b: Để A nguyên thì \(x-4\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{5;3;7;1\right\}\)
Bài 2:
a: \(=y\left(6x-y\right)\)
b: \(=x\left(y-2\right)+2\left(y-2\right)=\left(y-2\right)\left(x+2\right)\)
c: =(x+2)(x+5)

-Bài 3:
2) -Áp dụng BĐT Caushy Schwarz ta có:
\(A=\dfrac{1}{x^3+3xy^2}+\dfrac{1}{y^3+3x^2y}\ge\dfrac{\left(1+1\right)^2}{x^3+3xy^2+3x^2y+y^3}=\dfrac{4}{\left(x+y\right)^3}\ge\dfrac{4}{1^3}=4\)-Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)



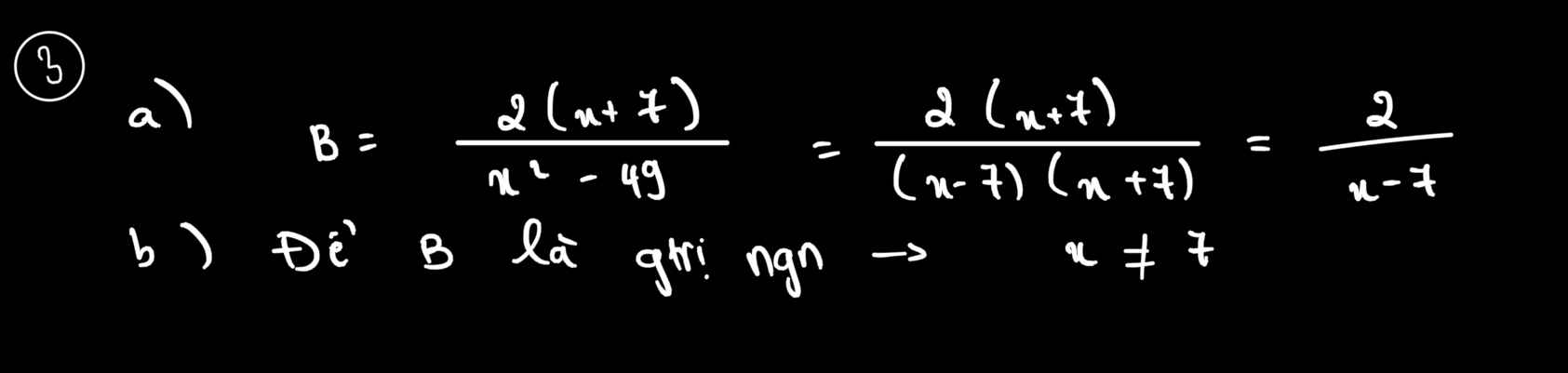
 mọi người giải hộ em ạ , em cảm ơn nhiều . Phần kia G
mọi người giải hộ em ạ , em cảm ơn nhiều . Phần kia G


Bài 1:
a: \(=-10x^3+20x^4-5x\)
b: \(=\dfrac{1}{3}a^2b+7a^5-1\)
c: \(=a^3+8+25-a^3=33\)
d: \(=x^2-16+8-x^3=-x^3+x^2-8\)
e: \(=a^3+1+8-a^3=9\)
f: \(=\dfrac{7-2x+4x-8}{2x+3}=\dfrac{2x-1}{2x+3}\)
g: \(=\dfrac{3}{2\left(x+3\right)}-\dfrac{2}{x\left(x+3\right)}\)
\(=\dfrac{3x-4}{2x\left(x+3\right)}\)