Question

[lên để hỏi thôi]

Hãy tính thể tích V, khối lượng m, khối lượng riêng D của một vật rắn biết rằng: khi thả nó vào một bình đầy nước thì khối lượng của cả bình tăng thêm là m₁ = 21,75 gam, còn khi thả nó vào một bình đầy dầu thì khối lượng của cả bình tăng thêm là m₂ = 51,75 gam (Trong cả hai trường hợp vật đều chìm hoàn toàn). Cho biết khối lượng riêng của nước là D1= 1g/cm³ , của dầu là D2 = 0,9g/cm³ .

Answer 1

[༺ ๖ۣۜPhạm ✌Tuấn ✌Kiệτ ༻]

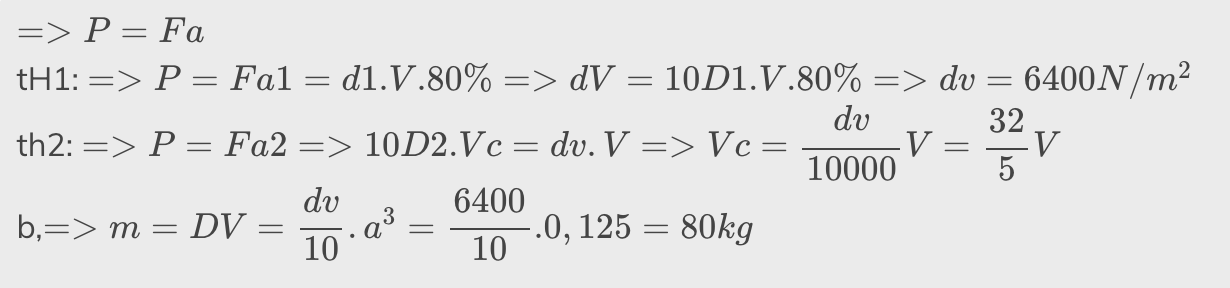
Gọi m, V, D lần lượt là khối lượng, thể tích, khối lượng riêng của vật. 
Khi thả vật rắn vào bình đầy nước hoặc bình đầy dầu thì có một lượng nước hoặc một lượng dầu ( có cùng thể tích với vật ) tràn ra khỏi bình. 
Độ tăng khối lượng của cả bình trong mỗi trường hợp: 
m₁ = m – D₁V    (1)
m₂ = m– D₂V    (2) 
Lấy (2) – (1) ta có:

m₂ – m₁ = V(D1 – D2) 
\(\Rightarrow V=\frac{m_2-m_1}{D_1-D_2}=300\) (cm³)
Thay giá trị của V = 300 cm³ vào (1), ta đc:

\(m=m_1+D_1V=321,75\left(g\right)\)

Từ công thức \(D=\frac{m}{V}\), ta có:

\(D=\frac{m}{V}=\frac{321,75}{300}\approx1,07\left(g\right)\)

Answer 2

[Nguyễn Thế Bảo]

Bạn xem lời giải của mình nhé:

Giải:

Gọi m, V, D lần lượt là khối lượng, thể tích, khối lượng riêng của vật.

Khi thả vật rắn vào bình đầy nước hoặc bình đầy dầu thì có một lượng nước hoặc một lượng dầu ( có cùng thể tích với vật ) tràn ra khỏi bình.

Độ tăng khối lượng của cả bình trong mỗi trường hợp:

m₁ = m – D_1.V (1)

m₂ = m – D_2.V (2)

Lấy (2) – (1) ta có: m₂ – m₁ = V.(D₁ – D₂)

\(\Rightarrow V=\frac{m_2-m_1}{D_1-D_2}=300\left(cm^3\right)\)

Thay giá trị của V vào (1) ta có : \(m=m_1+D_1.V=321,75\left(g\right)\)

Từ công thức \(D=\frac{m}{V}=\frac{321,75}{300}\approx1,07\)(g/cm³)

Vậy V = 300 cm³

m = 321,75g

\(D\approx\) 1,07g/cm³

Chúc bạn học tốt!