Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có P 1 x = P 1 . sin 30 0 = m 1 g . 1 2 = 0 , 15.10.0 , 5 = 0 , 75 ( N ) P 2 = m 2 g = 0 , 1.10 = 1 ( N )
Vậy P 2 > P 1 x vật hai đi xuống vật một đi lên, khi vật hai đi xuống được một đoạn s = 1m thì vật một lên cao z 1 = s . sin 30 0 = s 2 = 0 , 5 ( m )
Chọn vị trí ban đầu của hai vật là mốc thế năng
Theo định luật bảo toàn năng lượng
0 = W d + W t + A m s
W d = ( m 1 + m 2 ) v 2 2 = ( 0 , 15 + 0 , 1 ) v 2 2 = v 2 8 W t = − m 2 g s + m 1 g z 1 = − 0 , 1.10.1 + 0 , 15.10.0 , 5 = − 0 , 25 ( J ) A m s = F m s . s = μ m 1 g . cos 30 0 . s = 0 , 1.0 , 15.10. 3 2 .1 = 0 , 1299 ( J ) 0 = v 2 8 − 0 , 25 + 0 , 1299 ⇒ v ≈ 0 , 98 ( m / s )

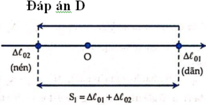
Lần 1 vật m đổi chiều:
Dây căng, vật M không dao động do vậy M trượt trên m từ vị trí lò xo dãn đến vị trí lò xo nén ![]()
Công của lực ma sát bằng độ biến thiên cơ năng của con lắc ta có:
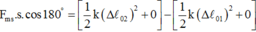
Thay số ta được:
![]()
![]()
![]()
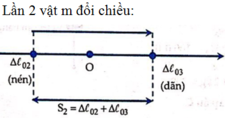
dây trùng, vật M dao động cùng với m, theo bảo toàn cơ năng vật sẽ đến vị trí mà lò xo dãn
![]()
Tính từ lúc thả đến khi m đổi chiều chuyển động lần thứ 2 thì quãng đường m đã di chuyển là
![]()

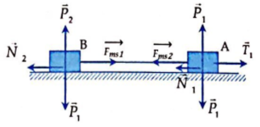
Hệ hai vật m 1 và m 2 chuyển động trong trọng trường, chỉ chịu tác dụng của trọng lực, nên cơ năng của hệ vật bảo toàn.
Vật m 1 , có trọng lượng P 1 = m 1 g ≈ 20 N và vật m2 có trọng lượng P 2 = m 2 g ≈ 1.10 = 10 N. Vì sợi dây nối hai vật này không dãn và P 1 > P 2 , nên vật m 1 chuyển động, thẳng đứng đi xuống và vật m 2 bị kéo trượt lên phía đỉnh mặt nghiêng với cùng đoạn đường đi và vận tốc. Như vậy, khi vật m 1 đi xuống một đoạn h thì thế năng của nó giảm một lượng W t 1 = m 1 gh, đồng thời vật m 2 cũng trượt lên phía đỉnh mặt nghiêng một đoạn h nên độ cao của nó tăng thêm một lượng hsinα và thế năng cũng tăng một lượng W t 2 = m 2 gh.
Theo định luật bảo toàn cơ năng, độ tăng động năng của hệ vật chuyển động trong trọng trường bằng độ giảm thế năng của hệ vật đó, tức là :
∆ W đ = - ∆ W t
⇒ 1/2( m 1 + m 2 ) v 2 = m 1 gh - m 2 gh.sin α
Suy ra W đ = 1/2( m 1 + m 2 ) v 2 = gh( m 1 - m 2 sin 30 ° )
Thay số, ta tìm được động năng của hệ vật khi vật m 1 đi xuống phía dưới một đoạn h = 50 cm :
W đ = 10.50. 10 - 2 .(2 - 1.0,5) = 7,5 J

Đáp án C
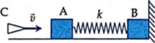
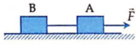
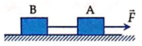
- Để B có thể dịch sang trái thì lò xo phải giãn một đoạn ít nhất là x0 sao cho:
![]()
![]()
- Như thế, vận tốc v0 mà hệ (m1 + m) có được ngay sau khi va chạm phải làm cho lò xo có độ co tối đa x sao cho khi nó dãn ra thì độ dãn tối thiểu phải là x0


Chọn mốc thế năng tại mặt nằm ngang BC
Theo định luật bảo toàn năng lượng
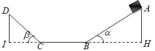
W A = W D + A m s M à W A = m g z A = m .10.1 = 10. m ( J ) W D = m g z D = m .10. z D = 10 m z D ( J ) A m s = μ m g cos α . A B + μ m g . B C + μ m g cos β . C D ⇒ A m s = μ m g ( cos 60 0 . A B + B C + cos 30 0 . C D )
⇒ A m s = 0 , 1.10. m ( cos 60 0 . A H sin 60 0 + B C + cos 30 0 . z D sin 30 0 ) = m ( 1 3 + 0 , 5 + 3 . z D ) ⇒ 10 m = 10 m z D + m ( 1 3 + 0 , 5 + 3 z D ) ⇒ 10 − 1 3 − 0 , 5 = 10 z D + 3 z D ⇒ z D = 0 , 761 ( m )

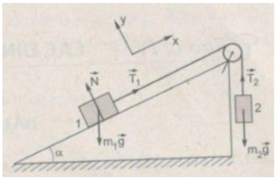
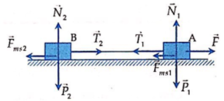
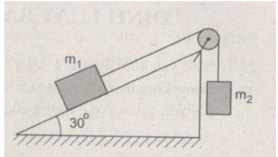
Chọn chiều dương của hệ tọa độ cho mỗi vật như hình vẽ
Xét vật 1:
Oy: N – m 1 gcos α = 0
Ox: T 1 – m 1 gsin α = m 1 a (1)
Xét vật 2:
M m 2 g – T 2 = m 2 a (2)
T 1 = T 2 = T (3)
Từ (1), (2) và (3) suy ra:
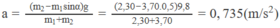
a > 0: vật m 2 đi xuống và vật m 1 đi lên.

Đáp án B
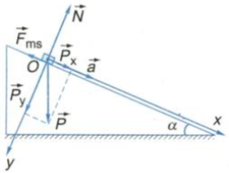
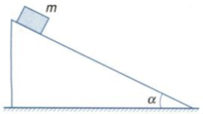
+ Có ba lực tác dụng lên vật khi vật trượt xuống mặt phẳng nghiêng:
Gồm trọng lực P ⇀ được phân tích thành hai thành phần Px→ và Py→ ; lực ma sát Fms→ ; phản lực N ⇀ .
+ Áp dụng định luật II Niuton, ta
có: P ⇀ + F m s ⇀ + N ⇀ = m.a→ (1)
+ Chọn hệ trục gồm: Ox hướng theo chiều chuyển động của vật: trên mặt phẳng nghiêng, Oy vuông góc với Ox và hướng xuống.
+ Chiếu biểu thức vecto (1) lên trục Ox, Oy ta được:
Theo trục Ox: Px – Fms = ma
⟺ Px – μ .N = ma (2)
Theo trục Oy: Py - N = 0 (3) (theo trục Oy vật không có gia tốc)
Thế (3) vào (2):
a = P x − μ . P y m = m g sin α − μ m g . cos α m = g ( sin α − μ . cos α )
Kết quả cho thấy gia tốc a của vật trượt có ma sát trên mặt phẳng nghiêng phụ thuộc vào g , μ , α
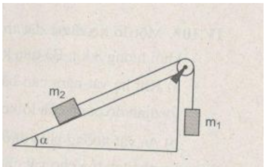


Ta có P 1 x = P 1 . sin 30 0 = m 1 g . 1 2 = 0 , 8.10.0 , 5 = 4 ( N ) P 2 = m 2 g = 0 , 6.10 = 6 ( N )
Vậy P 2 > P 1 x vật hai đi xuống vật một đi lên, khi vật hai đi xuống được một đoạn s = 50 cm thì vật một lên cao
z 1 = s . sin 30 0 = s 2 = 25 ( c m )
Chọn vị trí ban đầu của hai vật là mốc thế năng
Theo định luật bảo toàn năng lượng
0 = W d + W t + A m s V ớ i W d = ( m 1 + m 2 ) v 2 2 = ( 0 , 8 + 0 , 6 ) .1 2 2 = 0 , 7 ( J ) A m s = F m s . s = μ m 1 g . cos 30 0 . s = μ .0 , 8.10. 3 2 .0 , 5 = μ 2 3 ( J )
Vậy 0 = 0 , 7 − 1 + μ .2. 3 ⇒ μ = 0 , 0866