Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Do hai con chim vồ mồi cùng 1 lúc và với cùng một vận tốc nên quãng đường bay của 2 con pải như nhau
Gọi khoảng cách của con cá tới 2 gốc cây lần lượt là x,y(x,y>0)
Khoảng cách bay của con 1 là : \(\sqrt{20^2+x^2}\)\
Khoảng cách bay của con thứ 2 là \(\sqrt{30^2+y^2}\)
Do khoảng cách bằng nhau nên ta có pt:
\(\sqrt{30^2+y^2}=\sqrt{20^2+x^2}\)
\(\Leftrightarrow500=x^2-y^2=\left(x+y\right)\left(x-y\right)\)
\(\Leftrightarrow500=50\left(x-y\right)\)(do x+y=50)
\(\Leftrightarrow x-y=10\)
\(\Rightarrow\hept{\begin{cases}x+y=50\\x-y=10\end{cases}\Rightarrow x=30,y=20}\)
Vậy con trên cây cao 30 m có gốc cây cách con cá 20m
con trên cây cao 20m có gốc cây cách con cá 30m
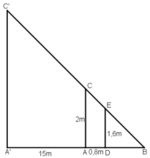
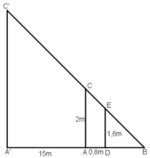
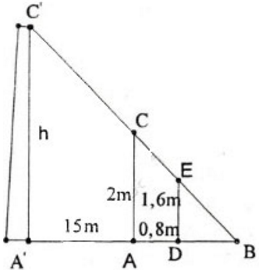
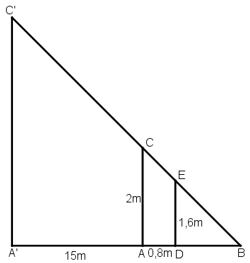
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB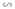 
ΔACB (vì DE // AC)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB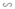 
ΔA’C’B (vì AC // A’C’)
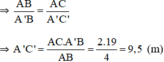
Vậy cây cao 9,5m.
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB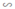 
ΔACB (vì DE // AC)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB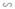 
ΔA’C’B (vì AC // A’C’)
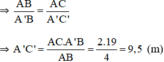
Vậy cây cao 9,5m.
Lời giải
Gọi chiều cao của cây là h = A'C' và chọn một cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Giải:
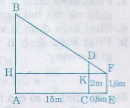
Giả sử AB là cây cần do, CD là cọc EF là khoảng cách từ mắt tới chân.
∆KDF ∽ ∆HBF
=> HBKD=HFKFHBKD=HFKF
=> HB = HF.KDKFHF.KDKF
mà HF = HK + KF =AC + CE = 15 + 0,8 = 15.8m
KD = CD - CK = CD - EF = 2 - 1,6 = 0,4 m
Do đó: HB = 7,9 m
Vậy chiều cao của cây là 7,9 m.
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
ΔACB (vì DE // AC)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB ΔA’C’B (vì AC // A’C’)
Vậy cây cao 9,5m.
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB ΔACB (vì DE // AC)
\(\Rightarrow\frac{DE}{AC}=\frac{DB}{AB}\)
Mà AC = 2m , DE = 1,6m
nên \(\frac{1,6}{2}=\frac{DB}{AB}\Rightarrow\frac{DB}{AB}=\frac{4}{5}\Rightarrow\frac{DB}{4}=\frac{AB}{5}\)
Áp dụng t/c DTSBN , ta có:
\(\frac{DB}{4}=\frac{AB}{5}=\frac{AB-DB}{5-4}=\frac{AD}{1}=0,8\)
Suy ra :
\(\frac{DB}{4}=0,8\Rightarrow DB=0,8.4=3,2\)
\(\frac{AB}{5}=0,8\Rightarrow AB=0,8.5=4\)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB ~ ΔA’C’B (vì AC // A’C’)
\(\Rightarrow\frac{AB}{A'B'}=\frac{AC}{A'C'}\)
\(\Rightarrow AC=\frac{AC.A'B'}{AB}=\frac{2.19}{4}=9,5\left(m\right)\)
Vậy cây cao 9,5m
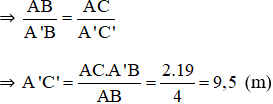
Giải
Giả sử AE là cây cọ cao 30m và BC là cây cọ cao 20m. Nếu gọi khoảng cách từ
gốc E đến con cá D là x (m) thì khoảng cách từ gốc C đến con cá D là: 50 - x (m)
Hai con chim cùng bay một lúc và vồ được cá cùng một lúc nên AD = BD
Theo định lí Pitago ta có:
30\(^2\) + x\(^2\) = 20\(^2\) + (50 – x)\(^2\)
900 + x\(^2\) = 400 + (2500 – 100 . x + x\(^2\))
Từ đó 100 . x = 2000, suy ra x = 20 (m)
Vậy con cá cách gốc cây cọ cao 30m là 20m