
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\left(\dfrac{1}{2}+\dfrac{1}{2}\right)-\left(\dfrac{5}{41}+\dfrac{36}{41}\right)=1-1=0\)

\(B=\dfrac{10\cdot9}{\sqrt{10}}-2\cdot5+1+2021=9\sqrt{10}-10+2022=9\sqrt{10}+2012\)

A= 3/4 +2/5-7/5+5/4
= (3/4 + 5/4) + (2/5-7/5)
= 2 + (-1)
= 1

a: f(-1)=5-3=2
f(3/2)=-15/2-3=-21/2
b: y=-8 thì -5x-3=-8
=>-5x=-5
hay x=1
y=0 thì -5x-3=0
=>-5x=3
hay x=-3/5


Cho tam giác ABC vuông tại A,AB<AC.Gọi M là trung điểm của BC.Kẻ đường thẳng d vuông góc tại BC tại M.đường thẳng d cắt AC tại D và cắt BA kéo dài tại E.
A) chứng minh tam giác BCD cân
B)Chứng minh BD vuông góc với EC
C) so sánh AD và DC
D)CHứng minh EM là trung tực của AK(K là giao điểm của BD và IC)
giúp em với huhuh lượt đăng bài cuối rồi

Gọi số hs thik thể thao, âm nhạc, thời trang ll là \(a,b,c(a,b,c\in \mathbb{N^*})\)
Áp dụng tc dtsbn:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=\dfrac{c-b}{5-3}=\dfrac{6}{2}=3\\ \Rightarrow\left\{{}\begin{matrix}a=6\\b=9\\c=15\end{matrix}\right.\)
Vậy ...
Gọi số hs thích thể thao; âm nhạc; thời trang lần lượt là \(x;y;z\)
Theo đề : \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}\) và \(z-y=6hs\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có :
\(\dfrac{z}{5}-\dfrac{y}{3}=\dfrac{z-y}{5-3}=\dfrac{6}{3}=2\)
Ta có : \(\dfrac{x}{2}=3\Rightarrow x=3.2=6\left(hs\right)\)
\(\dfrac{y}{3}=3\Rightarrow y=3.3=9\left(hs\right)\)
\(\dfrac{z}{5}=3\Rightarrow z=3.5=15\left(hs\right)\)
Vậy : Số hs thích thể thao : \(6hs\)
Âm nhạc : \(9hs\)
Thời trang: \(15hs\)

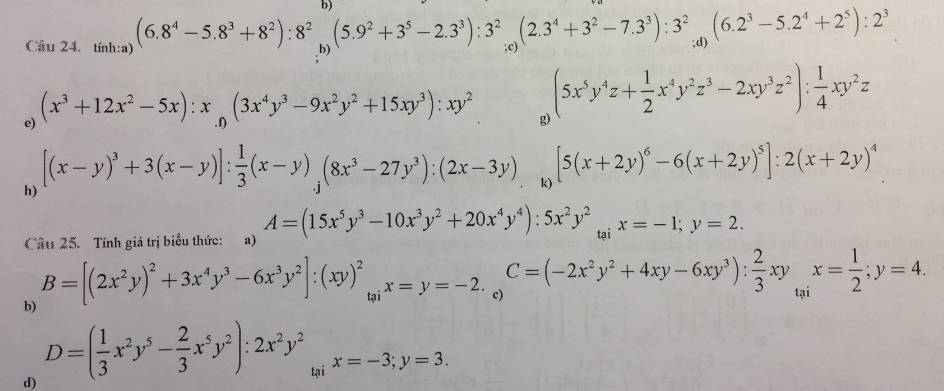
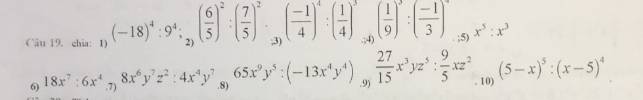 tớ đng cần gấp ý nên các cậu giúp tớ nhé....tớ camon trc ạaaaaaaa(nếu lm đc hết càng tốt ạ, có lời giải nhé)
tớ đng cần gấp ý nên các cậu giúp tớ nhé....tớ camon trc ạaaaaaaa(nếu lm đc hết càng tốt ạ, có lời giải nhé)
Lời giải:
Nếu $x+y+z+t=0$ thì $M=\frac{-t}{t}=\frac{-x}{x}=\frac{-z}{z}=-1$
$\Rightarrow (M-1)^{2025}=(-1-1)^{2025}=(-2)^{2025}$
Nếu $x+y+z+t\neq 0$. Áp dụng TCDTSBN:
$M=\frac{x+y+z}{t}=\frac{y+z+t}{x}=\frac{z+t+x}{y}=\frac{t+x+y}{z}=\frac{x+y+z+y+z+t+z+t+x+t+x+y}{t+x+y+z}=\frac{3(x+y+z+t)}{x+y+z+t}=3$
$\Rightarrow (M-1)^{2025}=2^{2025}$
cảm ơn, cảm ơnnn bạn nhiềuuu nha~