
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A=(-3/4+2/3).11/9+(-1/4+1/3):|-9/11|
\(=\left(-\frac{3}{4}+\frac{2}{3}\right).\frac{11}{9}+\left(-\frac{1}{4}+\frac{1}{3}\right).\frac{11}{9}\)
\(=\frac{11}{9}\left(-\frac{3}{4}+\frac{2}{3}-\frac{1}{4}+\frac{1}{3}\right)\)
\(=\frac{11}{9}\left(-1+1\right)\)
\(=\frac{11}{9}.0\)
=0


Gọi khối lượng giấy lớp 7A1 là a
khối lượng giấy lớp 7A2 là b
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{b-a}{4-3}=23\)
Do đó: a=69; b=92


a, Vì a//b mà a⊥AB nên b⊥AB
b, Vì a//b nên \(\widehat{CDB}+\widehat{ACD}=180^0\) (trong cùng phía)
Do đó \(\widehat{CDB}=180^0-120^0=60^0\)
c, Vì Ct là p/g nên \(\widehat{ICD}=\dfrac{1}{2}\widehat{ACD}=60^0\)
Xét tg CID có \(\widehat{CID}=180^0-\widehat{ICD}-\widehat{CDB}=180^0-60^0-60^0=60^0\)
d, Vì Dt' là p/g nên \(\widehat{BDt'}=\dfrac{1}{2}\widehat{BDy}=\dfrac{1}{2}\widehat{ACD}\left(đồng.vị\right)=60^0=\widehat{CID}\)
Mà 2 góc này ở vị trí so le trong nên Ct//Dt'

Bài 3:
1, Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{z-x}{3-6}=\dfrac{-21}{-3}=7\\ \Rightarrow\left\{{}\begin{matrix}x=42\\y=28\\z=21\end{matrix}\right.\)
2, Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{2x+3y-z}{6+15-7}=\dfrac{-14}{14}=-1\\ \Rightarrow\left\{{}\begin{matrix}x=-3\\y=-5\\z=-7\end{matrix}\right.\)
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x+y+z}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}}=\dfrac{130}{\dfrac{13}{12}}=120\)
Do đó: x=60; y=40; z=30





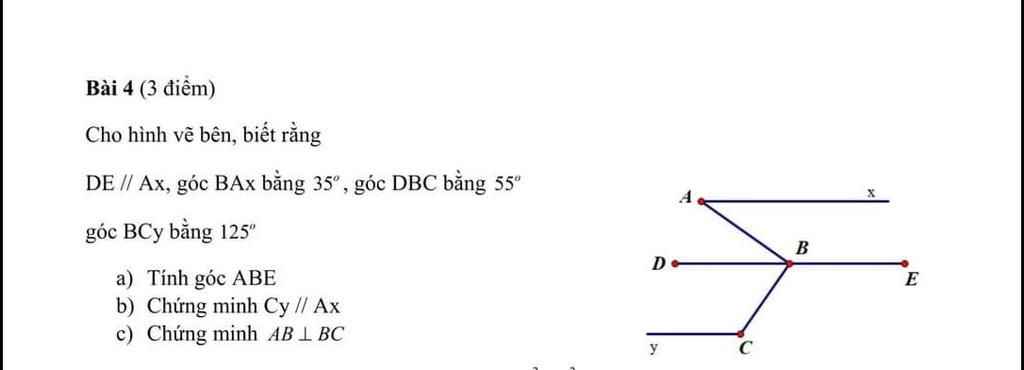

 lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!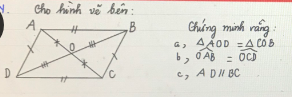
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{b-a}{4-3}=23\)
Do đó: a=69; b=92
Mình cảm ơn ạ