
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 6:
a: =12x^2+4x-3x-1-5x^2+15x-x^2+7x-12
=6x^2+23x-13
b: =5x^2+5x-2x-2-3x^3+3x^2+9x-2x(x^2-9x+20)
=-3x^3+8x^2+14x-2-2x^3+18x^2-40x
=-5x^3+26x^2-26x-2

Bài 3:
1, Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{z-x}{3-6}=\dfrac{-21}{-3}=7\\ \Rightarrow\left\{{}\begin{matrix}x=42\\y=28\\z=21\end{matrix}\right.\)
2, Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{2x+3y-z}{6+15-7}=\dfrac{-14}{14}=-1\\ \Rightarrow\left\{{}\begin{matrix}x=-3\\y=-5\\z=-7\end{matrix}\right.\)
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x+y+z}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}}=\dfrac{130}{\dfrac{13}{12}}=120\)
Do đó: x=60; y=40; z=30



Theo đề bài ta có:
;
cân bằng phương trình bằng cách nhân x vào cả hai vế ta có:
cân bằng phương trình bằng cách nhân y vào cả hai vế ta có:
cân bằng phương trình bằng cách nhân z vào cả hai vế ta có:
vì
Vì Có cùng số mũ và bằng nhau
Nên các cơ số cũng bằng nhau
Ta có: \(x^2=y\cdot z\)
nên \(z=\dfrac{x^2}{y}\)(1)
Ta có: \(y^2=z\cdot x\)
nên \(z=\dfrac{y^2}{x}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x^2}{y}=\dfrac{y^2}{x}\)
\(\Leftrightarrow x^3=y^3\)
hay x=y(3)
Ta có: \(x^2=y\cdot z\)
nên \(y=\dfrac{x^2}{z}\)(4)
Ta có: \(z^2=x\cdot y\)
nên \(y=\dfrac{z^2}{x}\)(5)
Từ (4) và (5) suy ra \(\dfrac{x^2}{z}=\dfrac{z^2}{x}\)
\(\Leftrightarrow x^3=z^3\)
hay x=z(6)
Từ (3) và (6) suy ra x=y=z(đpcm)
 giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ
giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ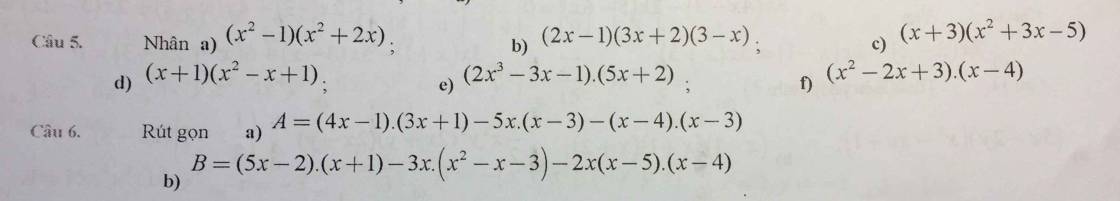
 lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!! GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
Tên tam giác là MNP
Tên 3 đỉnh là M,N,P
Tên 3 góc là \(\widehat{mNp};\widehat{nMp};\widehat{nPm}\)
Tên 3 cạnh là MN, NP, MP
* Tên tam giác: △MNP
* Tên 3 góc: góc M, góc N và góc P
* Tên 3 cạnh: cạnh MN, cạnh MP và cạnh NP
* Tên 3 đỉnh: đỉnh M, đỉnh N và đỉnh P.
Nếu bạn thấy đúng thì tick cho mình nha.