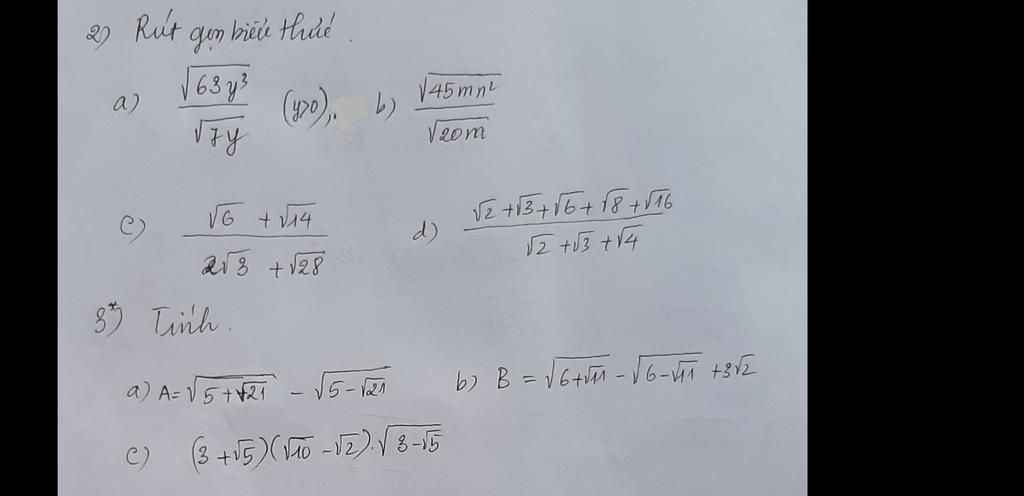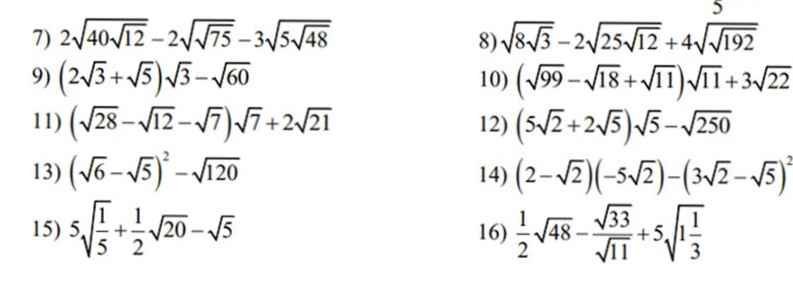K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NP
0
29 tháng 12 2021
2: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}=1\\\dfrac{1}{y}=\dfrac{4}{5}-\dfrac{1}{x}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{10}{3}\end{matrix}\right.\)
1 tháng 7 2021
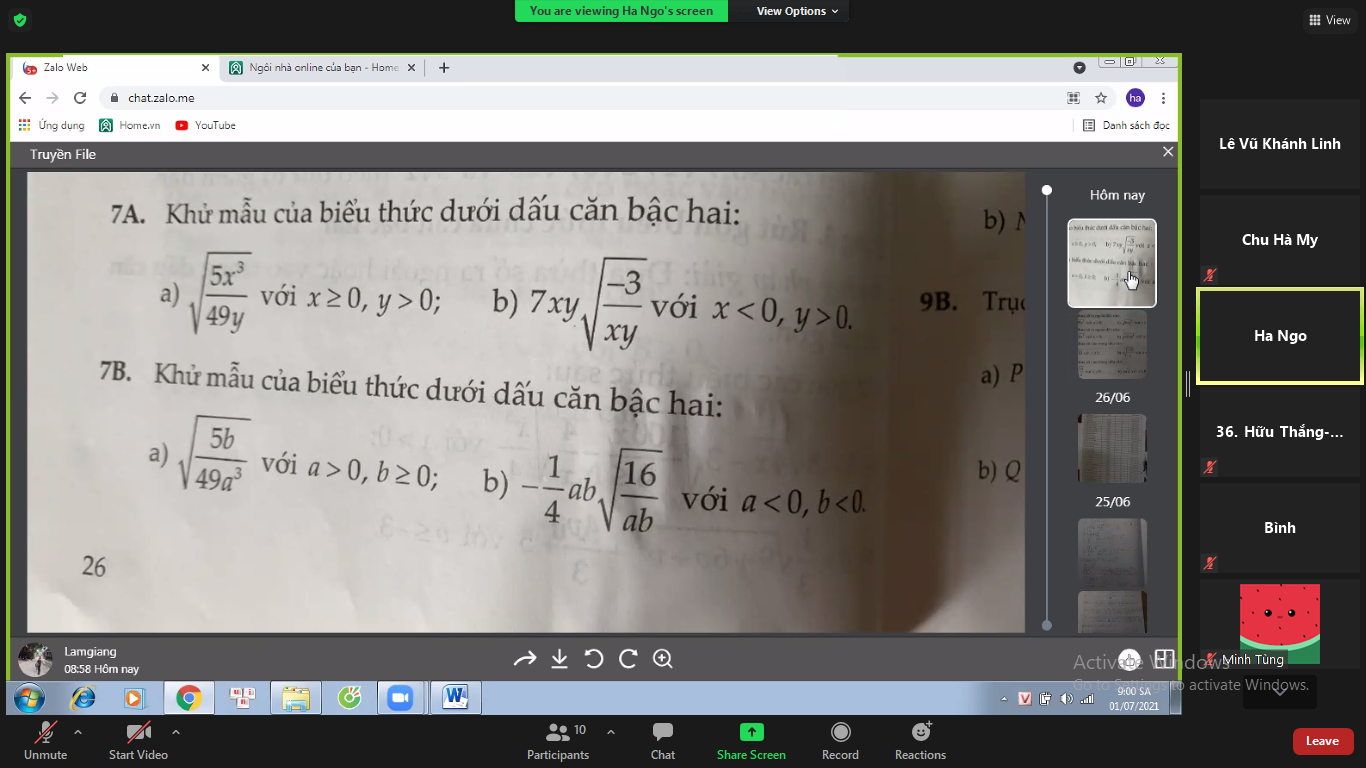
7A:
a) \(\sqrt{\dfrac{5x^3}{49y}}=\dfrac{\sqrt{5x^3}}{7\sqrt{y}}=\dfrac{\sqrt{5x^3y}}{7y}\)
b) \(7xy\sqrt{-\dfrac{3}{xy}}=7xy\cdot\dfrac{\sqrt{-3xy}}{xy}=7\sqrt{-3xy}\)
7B:
a) \(\sqrt{\dfrac{5b}{49a^3}}=\dfrac{\sqrt{5b}}{7a\sqrt{a}}=\dfrac{\sqrt{5ab}}{7a^2}\)
b) \(-\dfrac{1}{4}ab\sqrt{\dfrac{16}{ab}}=-\dfrac{1}{4}\cdot ab\cdot\dfrac{4\sqrt{ab}}{ab}=-\sqrt{ab}\)
27 tháng 8 2021
13: Ta có: \(\left(\sqrt{6}-\sqrt{5}\right)^2-\sqrt{120}\)
\(=11-2\sqrt{30}-2\sqrt{30}\)
\(=11-4\sqrt{30}\)
15: Ta có: \(5\sqrt{\dfrac{1}{5}}+\dfrac{1}{2}\cdot\sqrt{20}-\sqrt{5}\)
\(=\sqrt{5}+\sqrt{5}-\sqrt{5}\)
\(=\sqrt{5}\)
