
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+1=x-2\\y=x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-5\end{matrix}\right.\)

\(d,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=2+\sqrt{x+1}\\ \Leftrightarrow x-1=2+x+1+4\sqrt{x+1}\\ \Leftrightarrow4\sqrt{x+1}=-4\Leftrightarrow x\in\varnothing\left(4\sqrt{x+1}\ge0\right)\\ g,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow x+\sqrt{2x-1}+x-\sqrt{2x-1}+2\sqrt{\left(x+\sqrt{2x-1}\right)\left(x-\sqrt{2x-1}\right)}=2\\ \Leftrightarrow2x+2\sqrt{x^2-2x+1}=2\\ \Leftrightarrow\sqrt{\left(x-1\right)^2}=\dfrac{2-2x}{2}=1-x\\ \Leftrightarrow\left|x-1\right|=1-x\\ \Leftrightarrow\left[{}\begin{matrix}x-1=1-x\left(x\ge1\right)\\x-1=x-1\left(x< 1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x\in R\end{matrix}\right.\)

Bài 2:
Thay x=3 và y=-5 vào (d), ta được:
b-6=-5
hay b=1

\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)

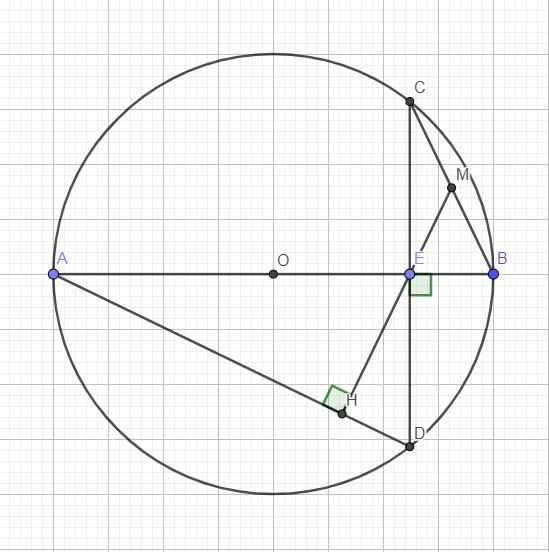
Tứ giác ACBD nội tiếp \(\Rightarrow\widehat{ADC}=\widehat{ABC}\) (cùng chắn AC) (1)
Lại có \(\widehat{ADC}+\widehat{DEH}=90^0\) (tam giác DEH vuông tại H theo gt) (2)
Gọi M là trung điểm BC, nối EM
Trong tam giác vuông BCE, EM là trung tuyến ứng với cạnh huyền
\(\Rightarrow EM=\dfrac{1}{2}BC=BM\Rightarrow\Delta BEM\) cân tại M
\(\Rightarrow\widehat{ABC}=\widehat{MEB}\) (3)
\(\left(1\right);\left(2\right);\left(3\right)\Rightarrow\widehat{DEH}+\widehat{MEB}=90^0\)
\(\Rightarrow\widehat{DEH}+\widehat{MEB}+\widehat{DEB}=90^0+90^0=180^0\)
\(\Rightarrow M;E;H\) thẳng hàng hay HE đi qua trung điểm M của BC

Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)


Bài 1:
a: Thay x=9 vào B, ta được:
\(B=\dfrac{2\cdot3+1}{3+2}=\dfrac{7}{5}\)
b: \(P=A:B\)
\(=\dfrac{2\sqrt{x}+1}{x-1}\cdot\left(\sqrt{x}-1\right)\cdot\dfrac{x+2}{2\sqrt{x}+1}=\dfrac{x+2}{\sqrt{x}+1}\)
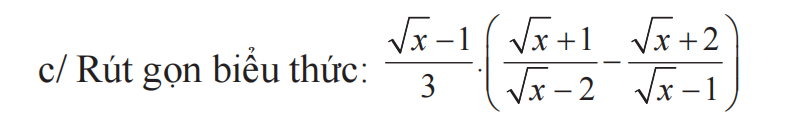



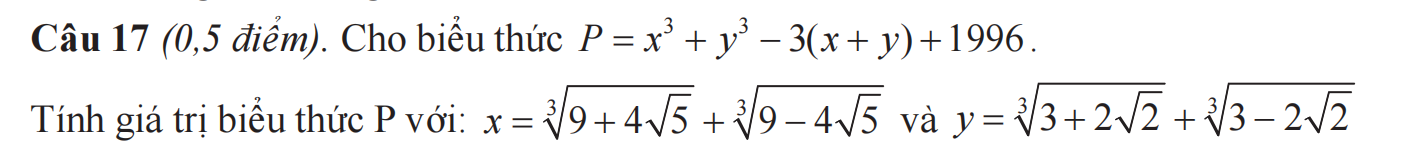 cảm ơn
cảm ơn 

 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
c) \(\dfrac{\sqrt{x}-1}{3}\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\)
\(=\dfrac{\sqrt{x}-1}{3}.\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}-1}{3}.\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)
\(=\dfrac{x-1}{3\left(\sqrt{x}-2\right)}-\dfrac{\sqrt{x}+2}{3}\)
\(=\dfrac{x-1}{3\left(\sqrt{x}-2\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{3\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-1}{3\left(\sqrt{x}-2\right)}-\dfrac{x-4}{3\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-1-x+4}{3\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{3\left(\sqrt{x}-2\right)}\)
\(=\dfrac{1}{\sqrt{x}-2}\)
bt trong dấu ngoặc bn nhân lên hợp ⇒ rút gọn ⇒ nhân với bt ngoài dấu ngoặc ⇒ rút gọn thôi á
mk gợi ý vậy thôi nha, chứ h giải ra thì lâu lắm=((
chúc bn làm bài tốt nka^3^